[컴퓨터비전#8/10-03] 경사하강법(Gradient Descent)과 Learning Late, Stochastic Gradient Descent
[컴퓨터비전#7/09-28] Linear Regression, 벡터화, feature map [컴퓨터비전#6/09-26] 기계학습의 종류와 개념, 손실함수, 손실함수와 파라메타 [컴퓨터비전#5/09-21] 그레디언트(엣지방향,강도), 소벨마스크 엣
devforyou.tistory.com
본 포스팅은 2022-10-05(수), 국민대학교 김장호교수님의 컴퓨터 비전 수업을 통해 배운내용을 정리하기 위한 게시글입니다.
또한 세종대학교 최유경교수님의 강의자료와 강의영상을 참고했습니다. 강의자료는 유튜브링크를 통해 더보기란 이동하여 github링크를 통해 확일 할 수 있습니다.
# 시작하기 전
10월05일에 학생예비군 때문에 수업을 듣지 못했다. 교수님께서 녹화강의를 올려주셨으나 음성녹음이 원활하지 않아서 영상을 보면서 공부 할 수 없었다. 그래서 다른 세종대학교의 최유경 교수님의 강의를 통해 공부했다. 세종대학교를 다니는 친구에게 예전에 추천받았는데 정말정말 강의력이 좋으시다.
# Classification (분류)
분류의 문제는 대표적인 지도학습(Supervised Learning)방법 중 하나로, 주어진 데이터들의 class를 파악하고 새롭게 들어오는 데이터에 대해서 분류를 하는 문제이다. 클러스터링은 비교사학습방법으로 데이터들을 스스로 어떠한 기준에 따라서 군집화를 이루는것과와는 대조된다고 볼 수 있다.
이번 시간에는 Binary Classification과 mulit-class classification에 대해서 알아볼 것이다.
## 개괄
먼저 분류를 위해서 Linear regression을 사용해보고 발생하는 문제점을 보완하기 위한 Logistic regression에 대해서 알아본다. 또한 Binary classification을 토대로 multi-class classification까지 사고의 확장을 해보도록 한다.
# Binary Classification
Binary는 이진의 뜻을 가진다. 예/아니오와 같이 2가지로 답을 내릴 수 있는 경우다. Spam/Ham , 양성/음성과 같이 범주형 데이터를 가지게 된다. 이러한 범주형 데이터를 가지기 때문에 숫자의 형태로 라벨링이 필요 하다. 예를들어 Spam(1) / Ham(0) , 양성(1) / 음성(0)처럼 말이다. 이러한 것을 Encoding이라고 표현한다.
# using Linear Regression
그렇다면 이진분류를 위해서 Linear Regression(선형회귀)를 적용해보자. 선형 회귀는 H(x) = Wx꼴을 가지게 되며 선형으료 표현 될 것이다. 시험공부시간에 따른 pass / fail의 예제를 봐보자.

현재 데이터를 기준으로 선형회귀를 시키면 그림과 같은 Wx가 표현될 것이다. 0.5의 기준치를 토대로 pass/fail이 구별되고 있다.
50시간 공부 / Pass라는 데이터가 추가된다. 그리고 Linear Regression을 해보자.
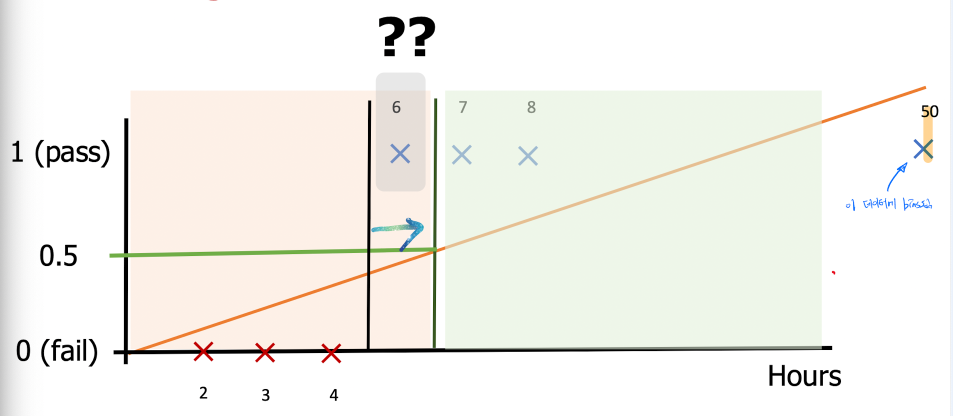
Linear Regression의 값은 이 50이라는 값의 매우 bias하게 된다. 우리가 기존의 0.5로 잡았던 임계점을 토대로 다시 값을 본다면 6시간 데이터는 fail이라는 예측이 나와버린다. 뭔가 대단히 잘못됐다는 것을 느낀다.
## Sigmoid를 이용한 개선
우리는 Y값 즉 binary classification에 의해서 예측결과가 0또는1이라는 사실을 알 수 있다. 쉽게 말해 Spam/Ham과 같이 둘중 하나의 ouput값이 나온다는 사실이다.
그러나 우리가 Linear Regression에 의한 output은 1을 넘어설수도 있고 0보다 작아 질 수 도 있다.

x가 1,2,5,10이라는 데이터로 얻어낸 w=0.5 b=0이라는 모델에 새로운 input x를 넣게되면 y는 50이라는 1보다 큰 숫자가 나온다. 가설을 재설정해야한다. 우린 이 y가 즉, 0<= H(x) <= 1이라는 범위를 가질 수 있도록 해야할 것이다.
신기하게도 Sigmoid라는 함수는 0과1사이의 범위만을 가진다. 이를 이용해 Logistic funciton을 만들어 낼 수 있다.

그렇다면 이 sigmoid함수에 H(x) = Wx, 즉 Wx를 넣어준다면 0과 1사이의 범위를 가지는 함수가 생길 것이다.

이제 H(x)의 값은 0<= H(x) <= 1을 충족시킨다.
## Cost function

그러나 이렇게 얻은 Logistic funcion에 기존에 있던 손실함수를 사용하게 되면 global minimum을 구할 수 없게 된다. 손실함수가 convex형태가 아니기에 local minimum에 빠지게 되기 때문이다. 그렇다면 바뀐 가설에 맞게 Cost Function도 재설계 할 수 있어야 한다.

손실함수는 정답값과 가까워질수록 손실함수의 값이 작아지고, 정답값과 멀어질수록 손실함수의 값이 커진다. 이 새롭게 얻은 손실함수를 통해서 한번 확인해보자.
맞춰야하는 정답값이 y=1인경우는 파란색함수(-logh), 정답값이 y=0인경우에는 빨간함수(-log(1-h)를 따르게 된다. 우리가 맞춰야하는 값이 y=1인경우, H(x)가1이라면 손실함수의 값은 0이 된다. 반대의 경우 맞춰야하는 값이 y=1인경우, H(x)의 값이 0이라면 손실함수는 무한대에 수렴한다. 즉 맞췄다면 손실함수가 작고 틀렸다면 커지는 손실함수의 경향성에 만족함을 알 수 있다.
이런 조건부로 나누어진 이 손실함수는 우리가 컴퓨터로 사용하기에는 좋지 않기때문에 풀어보면 아래와 같은 값을 가짐을 알 수 있다.

이렇게 얻은 손실함수를 통해서 경사하강법을 사용한다면 그 수식은 아래와 같을 것이다.
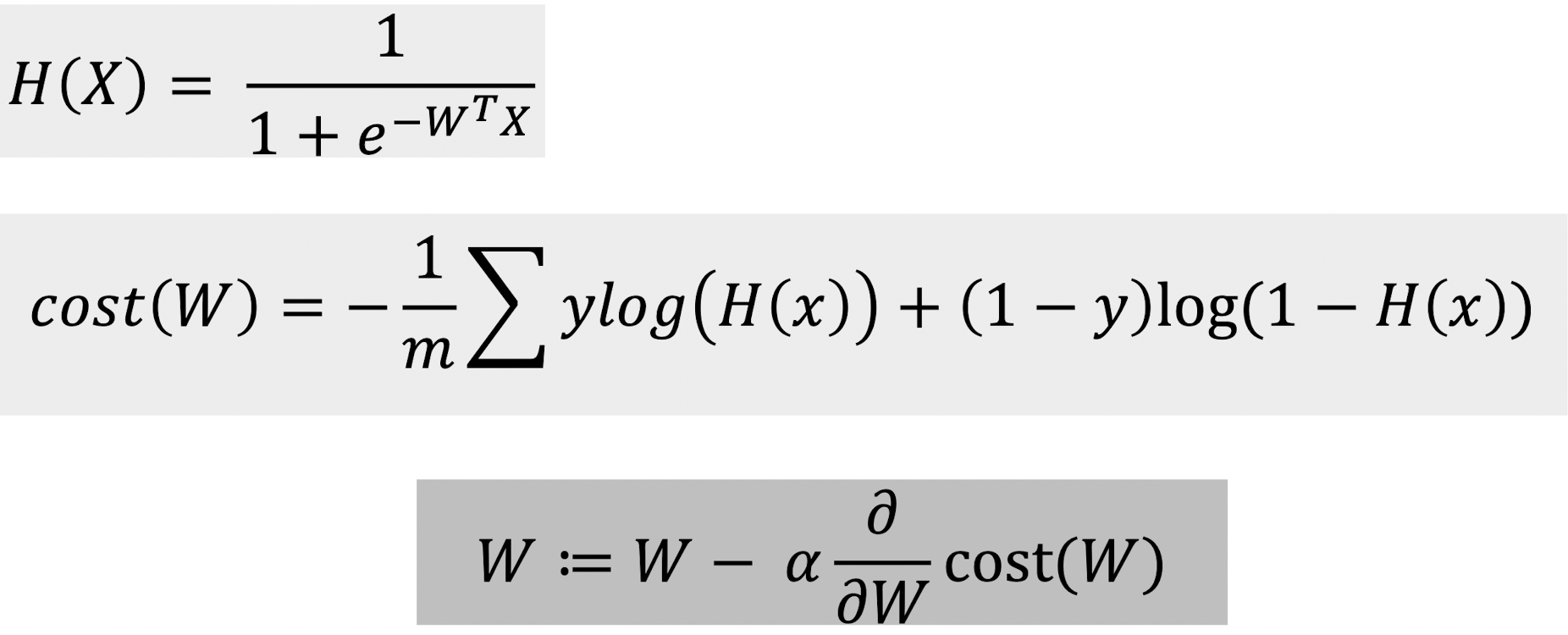
즉 아래와 같이 분류의 문제를 시그모이드함수를 통해서 해결 할 수 있게 됐다.


# multi-class classification
Multi-calss classificaiton은 binary classification을 사용해서 해결 할 수 있다. binary classification는 A / B 로 나눴던 분류방식을 A / not A이와 같이 생각하면 된다. 즉 우리가 A, B, C 세가지를 분류해야 한다면, 3번의 binary classification을 거치면 된다. 3번의 질문을 통해서 해결 할 수 있을 것이다. C를 찾아야 한다면 C에 대해서 A를 판정하는 질문을 던지면 A / or not , B / or not , C / or not이라는 세 질문에 대해서 or not, or not C라는 대답을 통해서 C임을 알 수 있을 것이다.

그럼 이 질문은 3가지의 분류기를 통과하는 것과 같다.
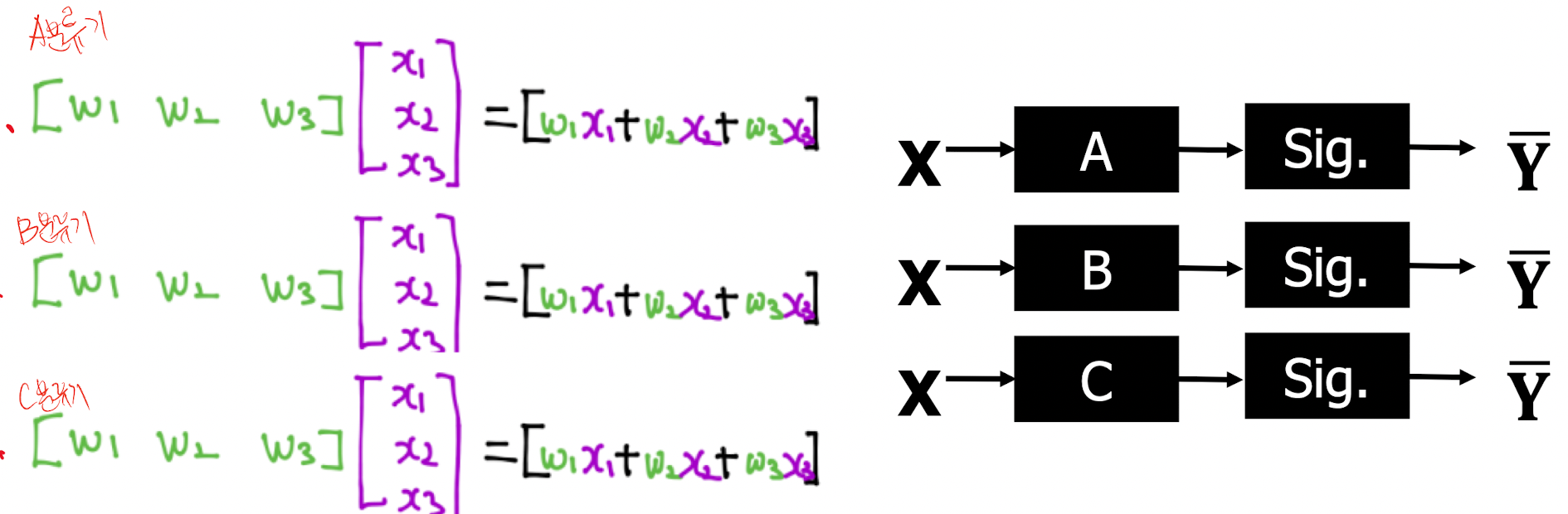
이를 아래와 같이 재표현 할 수 있다.
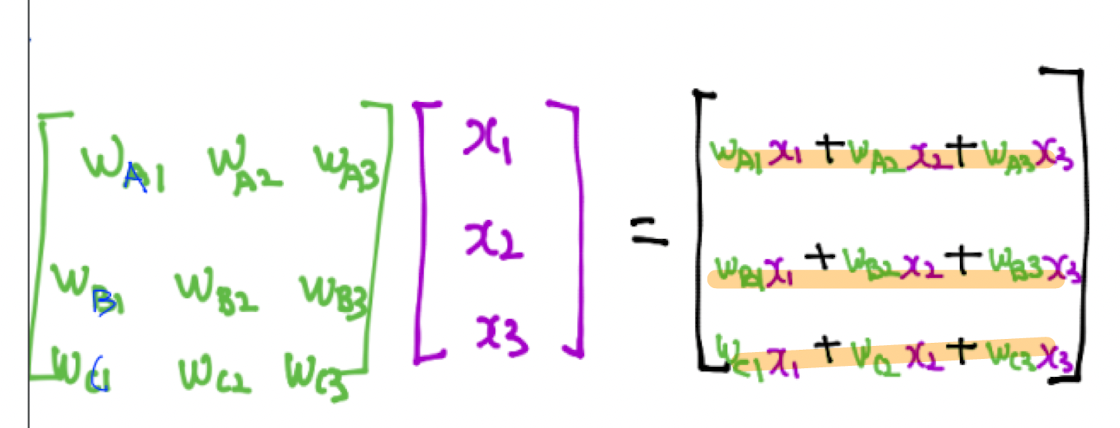
그러나 이렇게 분류기를 거쳐서 나오는 값을 바로 사용하면 문제가 발생함수 있기에 softmax를 사용해서 정규화 시킨 값을 사용해야 한다.
또한 손실함수로써는 Cross-entropy를 사용한다.
# 참고
수학포기자를 위한 딥러닝-#4 로지스틱 회귀를 이용한 분류 모델
수포자를 위한 딥러닝 #4 - 로지스틱 회귀를 이용한 이항 분류 문제의 해결 조대협 (http://bcho.tistory.com) 1장에서 머신러닝의 종류는 결과값의 타입이 연속형인 Regression (회귀) 문제와, 몇가지 정해
bcho.tistory.com
'•Compter Science > Computer Vision' 카테고리의 다른 글
| [컴퓨터비전#11/10-31] L1놈과 L2놈을 이용한 Regularization(정규화) (0) | 2022.10.31 |
|---|---|
| [컴퓨터비전#10/10-09] 로지스틱 회귀 손실함수, 이진 크로스엔트로피 미분하여 경사하강법 도출, 소프트맥스 함수, one-hot-encoding (0) | 2022.10.11 |
| [컴퓨터비전#8/10-03] 경사하강법(Gradient Descent)과 Learning Late, Stochastic Gradient Descent (3) | 2022.10.04 |
| [컴퓨터비전#7/09-28] Linear Regression, 벡터화, feature map (0) | 2022.09.29 |
| [컴퓨터비전#6/09-26] 기계학습의 종류와 개념, 손실함수, 손실함수와 파라메타 (2) | 2022.09.28 |
![[컴퓨터비전#9/10-05] Classification, Linear Regression, Logistic Regression, sigmoid](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbXQ5HG%2FbtrN9rVKj0Y%2FaE3Bz6v5zjCSc8bZ79qCak%2Fimg.png)