[컴퓨터비전#14/11-16] 1*1 Convolution, pooling, conv의 output과 wieght개수 계산, Batch-Normalization
[컴퓨터비전#13/11-14] Convolution Layer- 필터(Feature-map,padding,stride) [컴퓨터비전#12/11-07] 오류역전파방법, 모듈로 사고의 확장, dropout, earlystop [컴퓨터비전#11/10-31] L1놈과 L2놈을 이용한 Regularization(정규
devforyou.tistory.com
본 포스팅은 2022-11-21(월), 국민대학교 김장호 교수님의 컴퓨터 비전 수업을 통해 배운내용을 정리하기 위한 게시글입니다.
# Batch Normalization
저번 시간에 공부하다가 만 Batch Normalization에 대해서 조금 더 알아보자. Batch Normalization은 배치단위로 정규화를 수행하는 것이다.
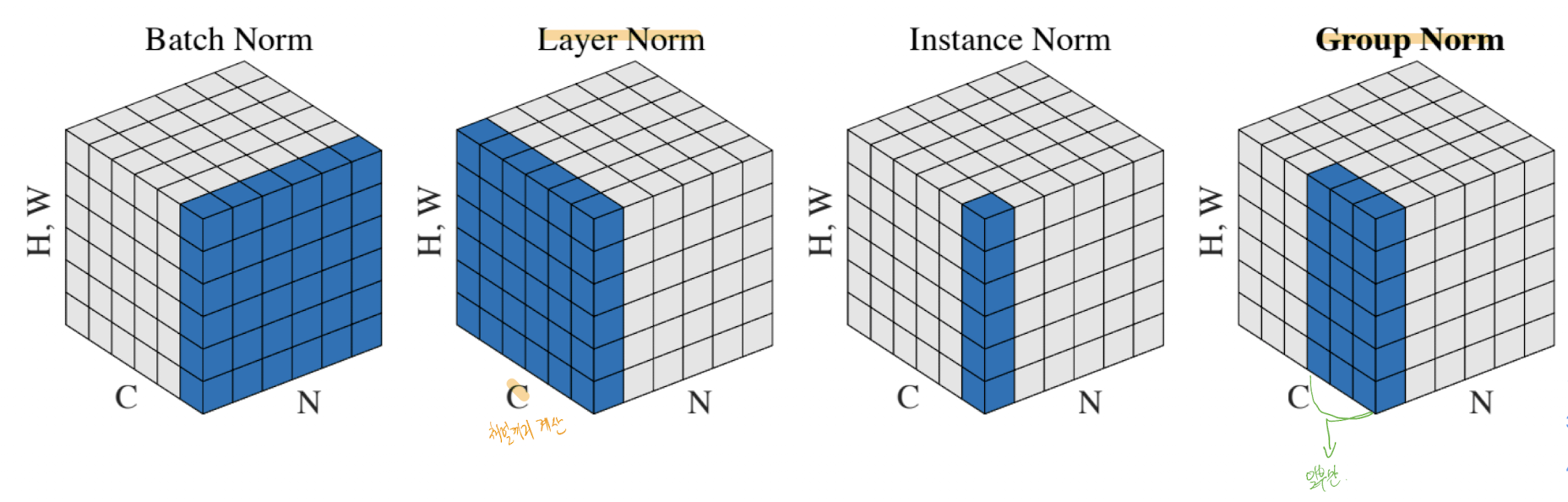
## Batch Norm
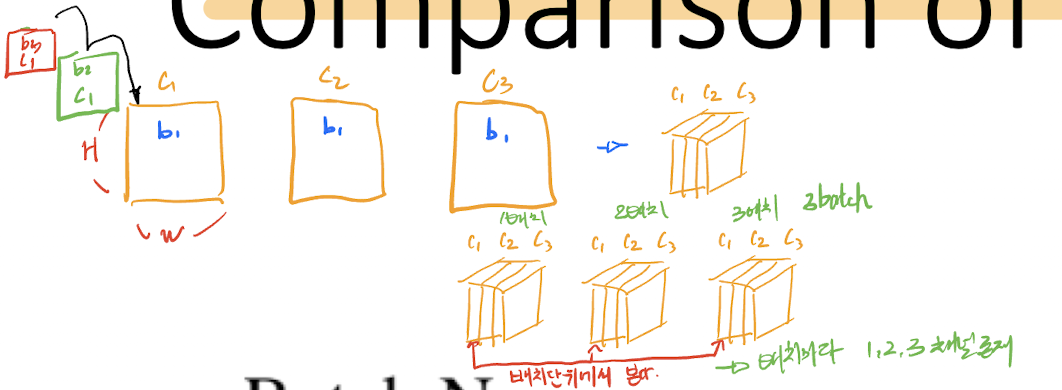
배치 단위로 정규화는 한다는 것은, 보는 데이터가 배치갯수(N)이 된다. 한 데이터 input이 3개의채널로 이루어져 있을때, 이렇게 3개의 채널로 이루어진 데이터가 N(배치)개가 존재하게 된다. 그럴 때, 배치단위로 본다는 것은, 1번데이터 C1 , 2번데이터 C1, 3번 데이터 C1 .. N번 데이터 C1을 함께 보게 되는 것이고, 채널 갯수만큼 보게 된다.
그렇다면 CNN의 구조에서는 이러한 채널이 들어 있기 때문에, 아래와 같이 normalize를 계산할 수 있다.
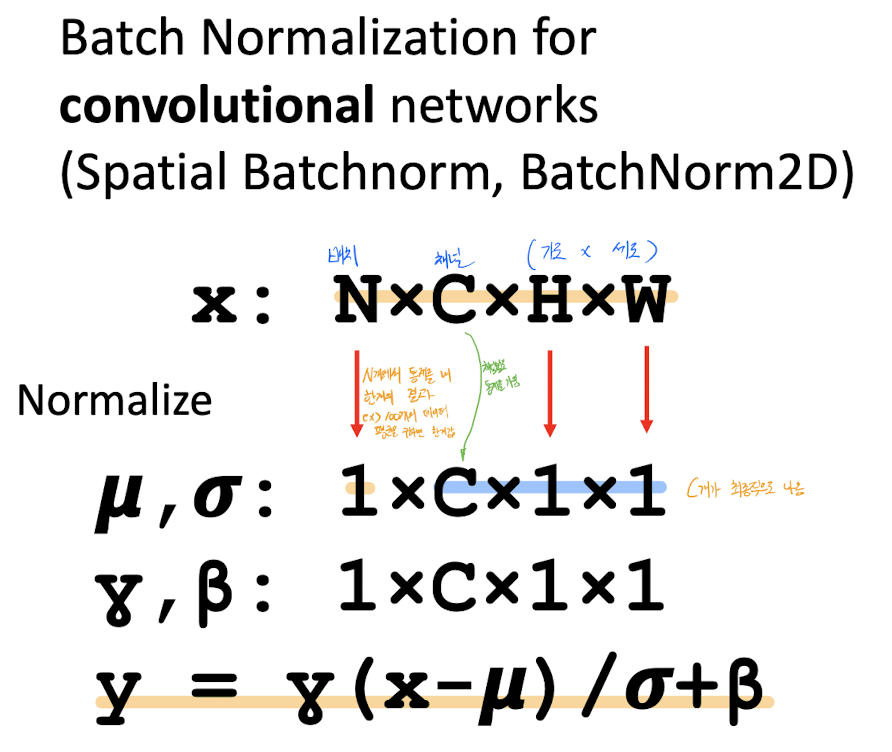
입력에 대해서 N개에서 채널끼리 보기 때문에 최종 C개가 나온다.
## Layer Norm
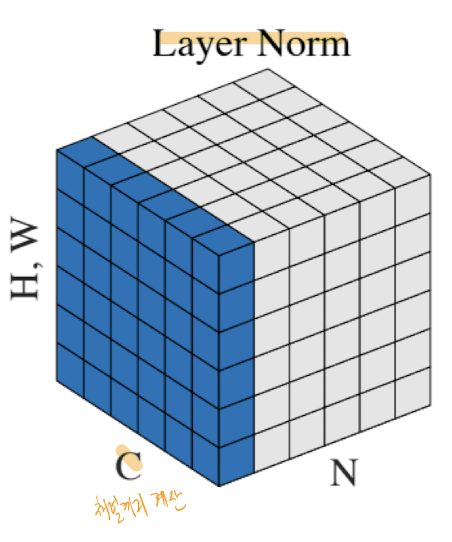
Layer는 채널끼리를 봐버 리기 때문에, N개가 된다. 아래 식은 FC예시지만, D이제 ( Channel * H * W )일 경우 CNN이고, 그럴 경우에도 결국 N이 된다.

# vector_backprop
[컴퓨터비전#12/11-07] 오류역전파방법, 모듈로 사고의 확장, dropout, earlystop
[컴퓨터비전#11/10-31] L1놈과 L2놈을 이용한 Regularization(정규화) [컴퓨터비전#10/10-09] 로지스틱 회귀 손실함수, 이진 크로스엔트로피 미분하여 경사하강법 도출, [컴퓨터비전#9/10-05] Classification, Linear
devforyou.tistory.com
지난 시간에 배웠던 역전파 방법은, 스칼라인 상황에서만이었다. 그러나 실제 영역에서는 벡터, 매트릭스끼리의 역전파가 이루어지기 때문에 조금은 복잡해진다. 먼저 위 정리글을 한번보고나서 다시 공부해야 했다.
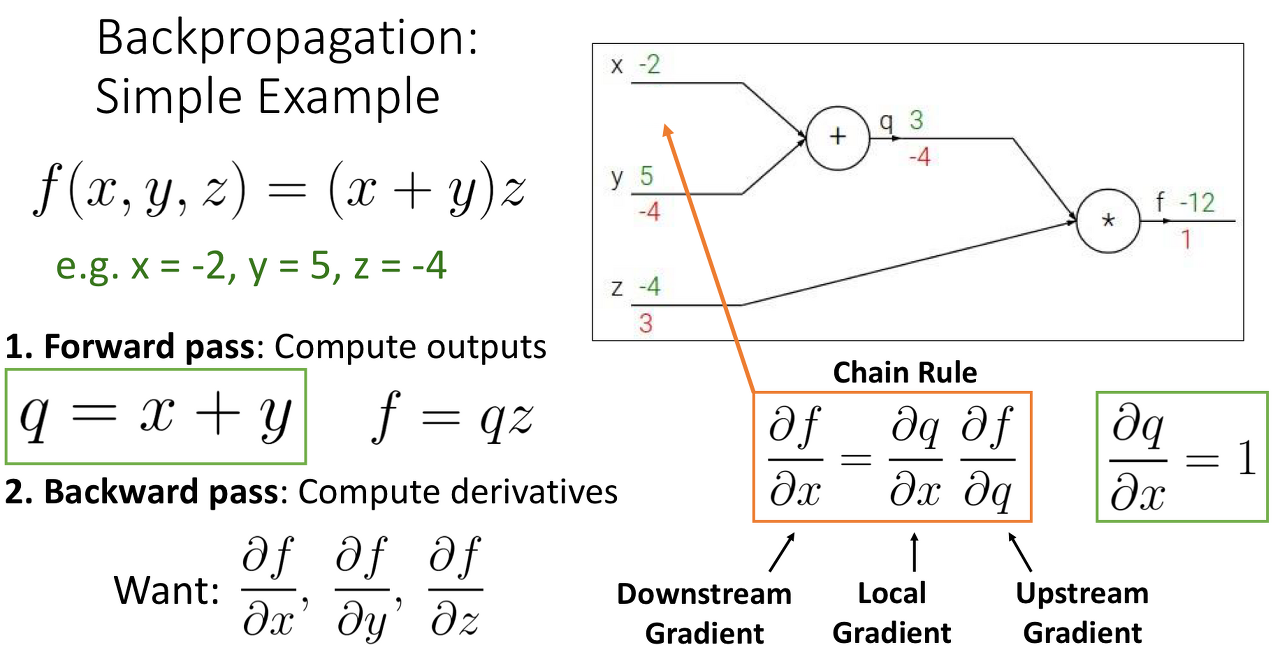
먼저 ChainRule에서 Upstream-Gradient와 Local-Gradient, Downstream-Gradient가 어떤 역할을 하고 왜 나오게 됐는지를 이해한다면 그렇게 어렵지 않을 것이다.
## 자코비안

스칼라,스칼라의 미분은 일반적인 미분이었다면, 입력이 N차원 출력이 스칼라일때는, 그래디언트였다. x,y모두가 N차원이라면 이를 자코비안이라고 한다.
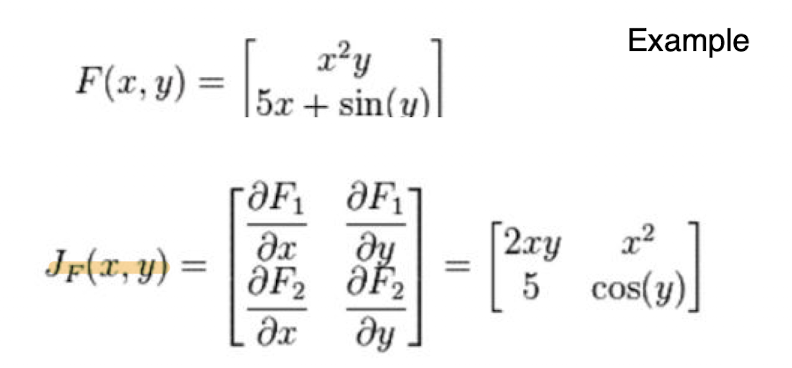
그냥 한번 더 미분해준 거다.
# 역전파 - 벡터
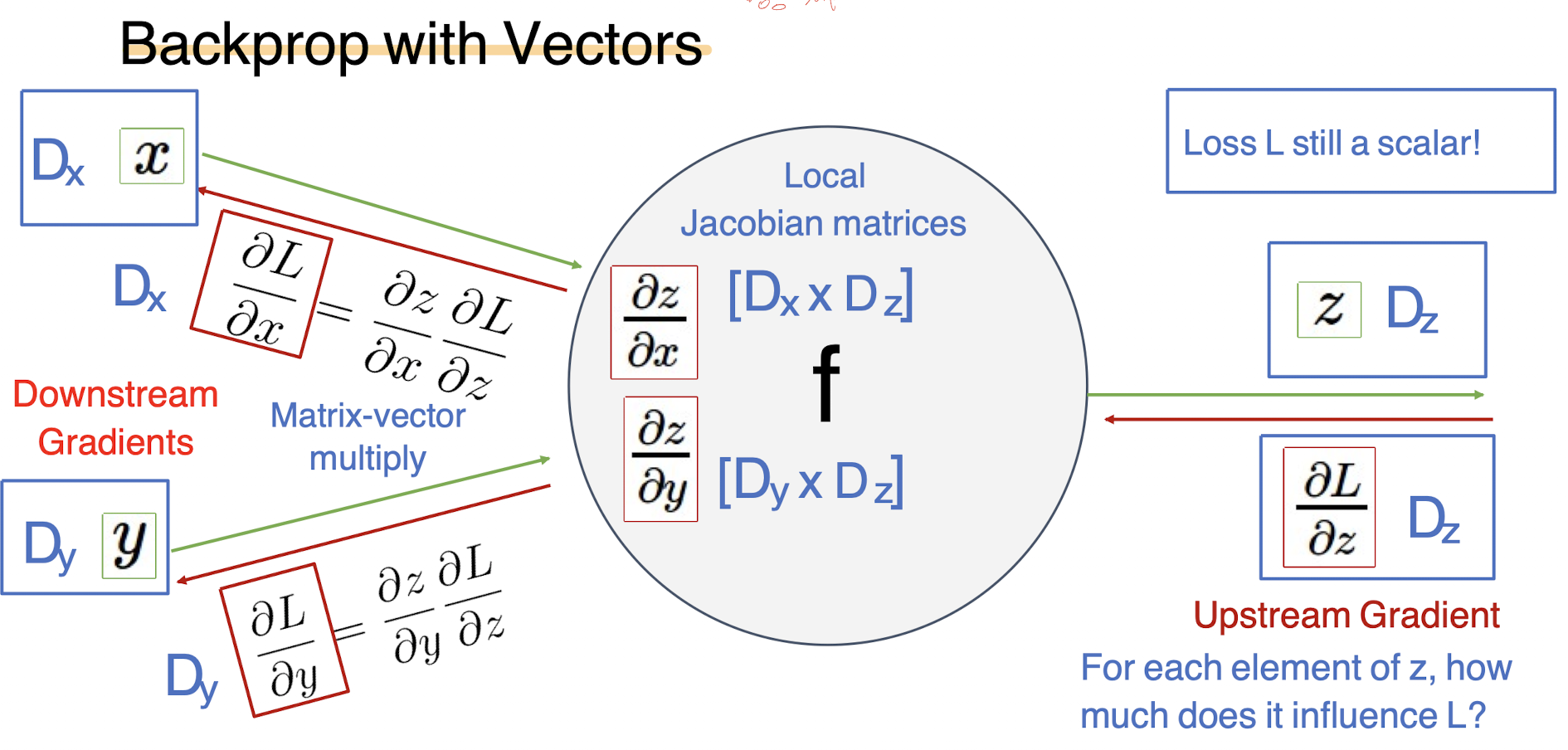
다음과 같은, x나 y의 그래디언트를 찾아야 한다고 했을때, dL/dz의 업스트림그래디언트를 로컬그래디언트에 곱해서 얻어낼 수 있다. 그러나 입력값이 벡터라면, 이 LocalGradeint를 구할때 자코비안행렬이 나오고 그 크기는 Dx * Dz가 된다.
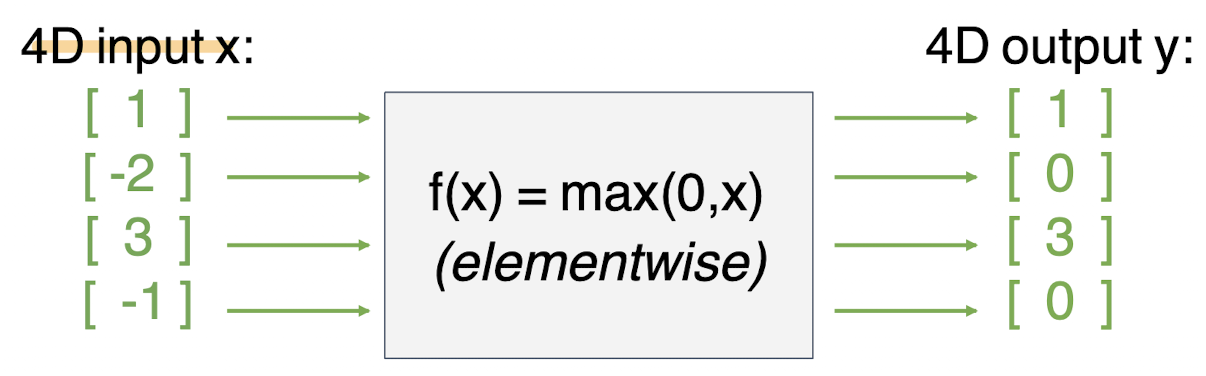
다음과 같이 ReLu를 거쳤다고 가정했을때, 어떻게 구해지는 봐보자.
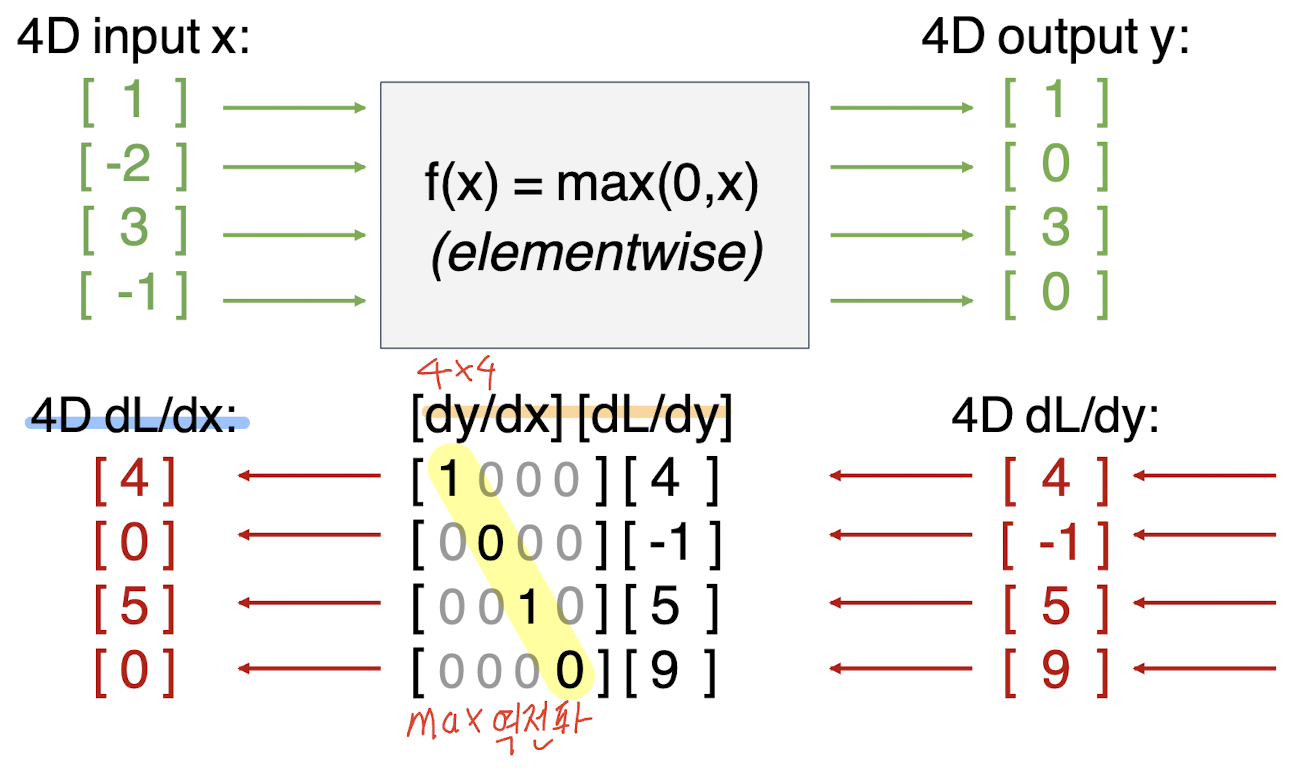
4*4의 자코비안이 나오게 된다.
# 역전파 - 행렬(or Tensor)
이제 인풋과 output이 행렬이라면 어떻게 될까? vector와 비슷하다.
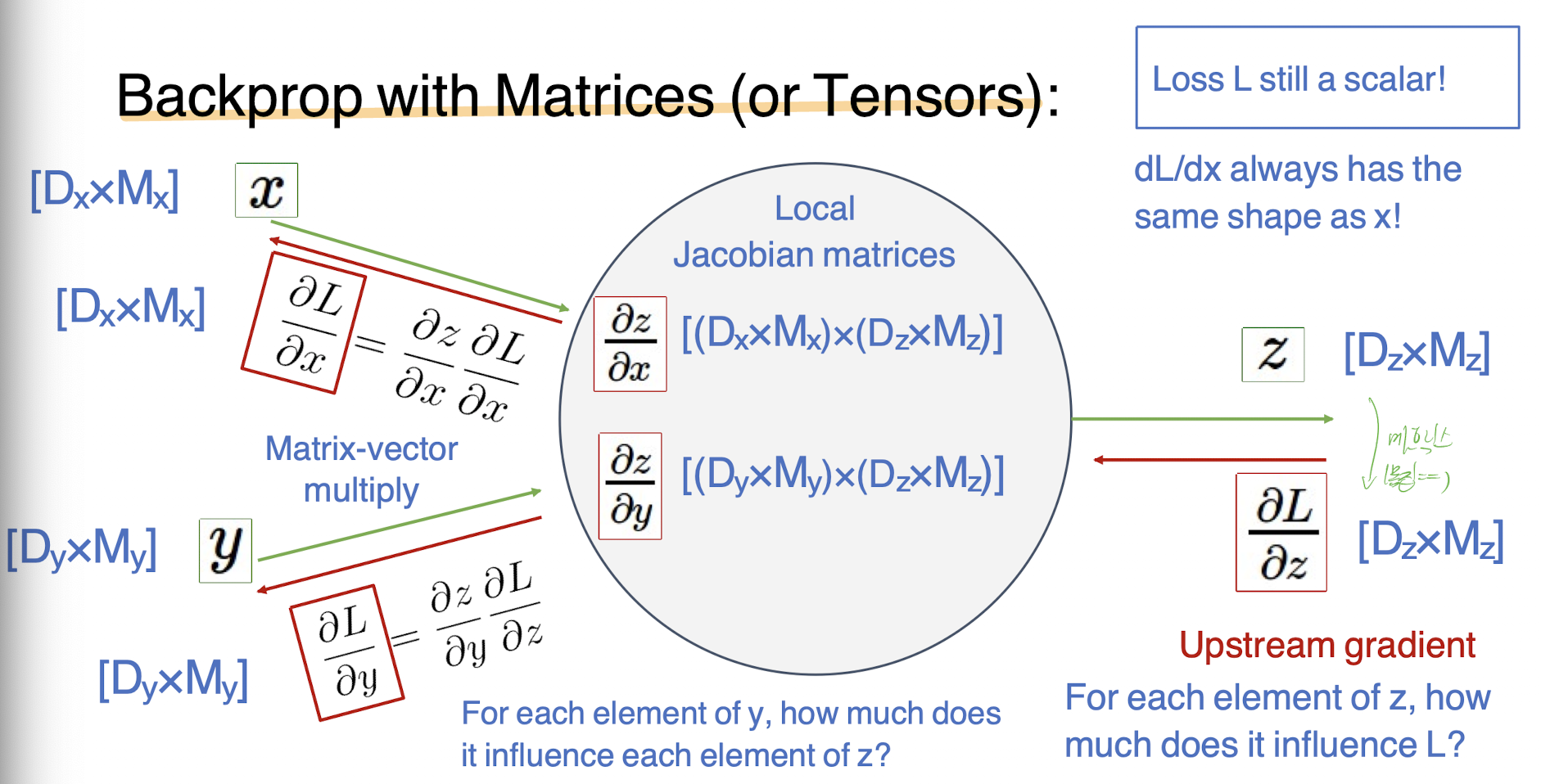
x => Dx * Mx 이고 z=> Dz * Mz이다. 그래서 Local Jacobian은 위 벡터와 똑같이 두개의 크기가 이용된다.
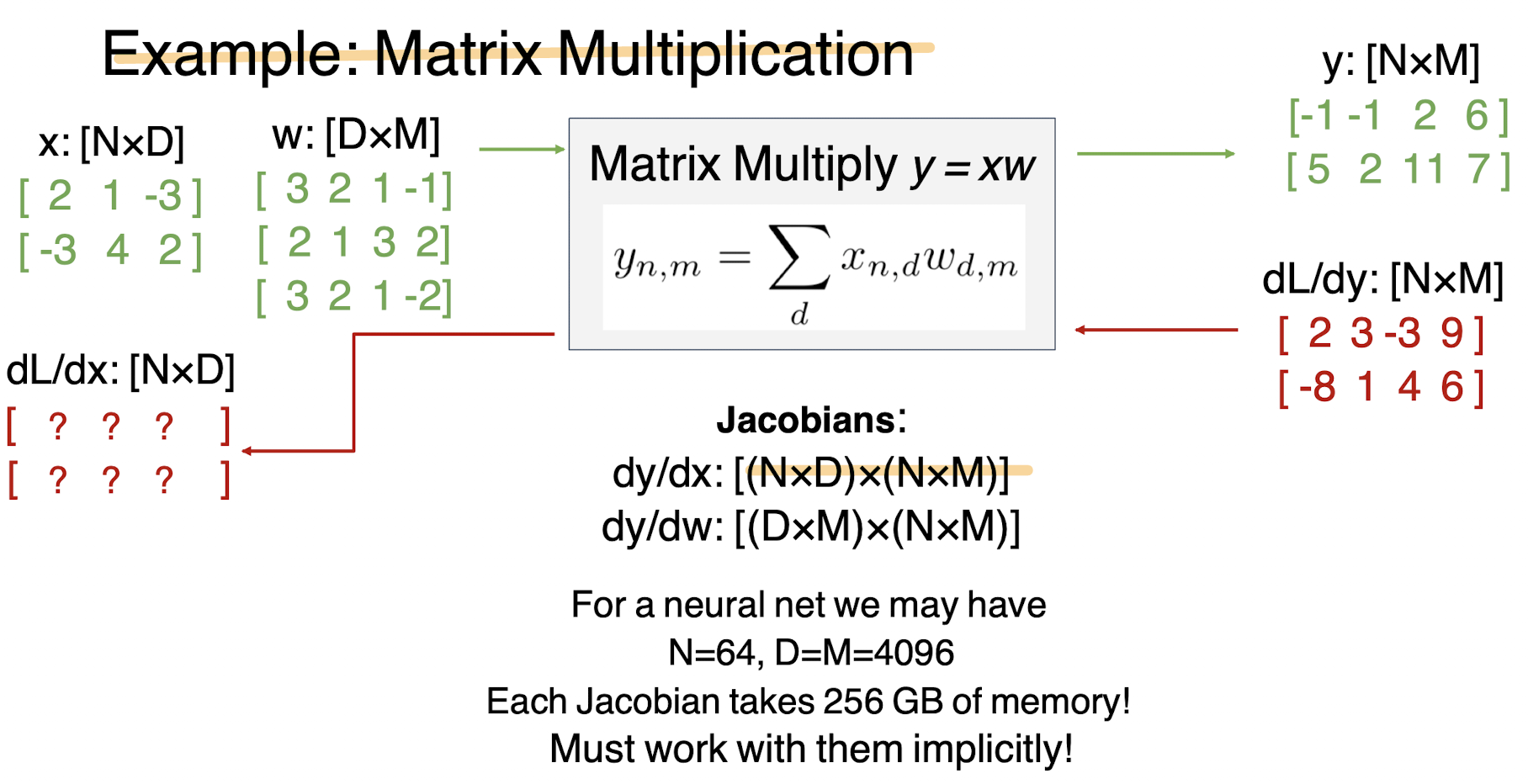
즉 dL/dx를 구하기 위해서 [(N*D) * (N*M)]의 메모리 공간이 필요하게 된다. 위에서 써있는것처럼의 예시라면 256기가나 필요하다고 한다. 정말 엄청난 양 이다.
그러나 굳이 자코비안을 쓰지 않고도 구할 수 있기 때문에 그 방법을 알아보도록 하자.
# 자코비안을 쓰지 않고 구하는 방법
그래디언트는 해당 값이 연산에 기여를 했다면 무조건적으로 존재하게된다. 그러면 구하려는 그래디언트가 어디에 기여를 했는지를 안다면 쉽게 구할 수 있을 것이다.
dL/dx(1,1)을 구해보자.

위와 같이 Local Gradeinet Slice를 활용해서 풀 수 있는데, 아래에 손으로 정리 해 봤다.
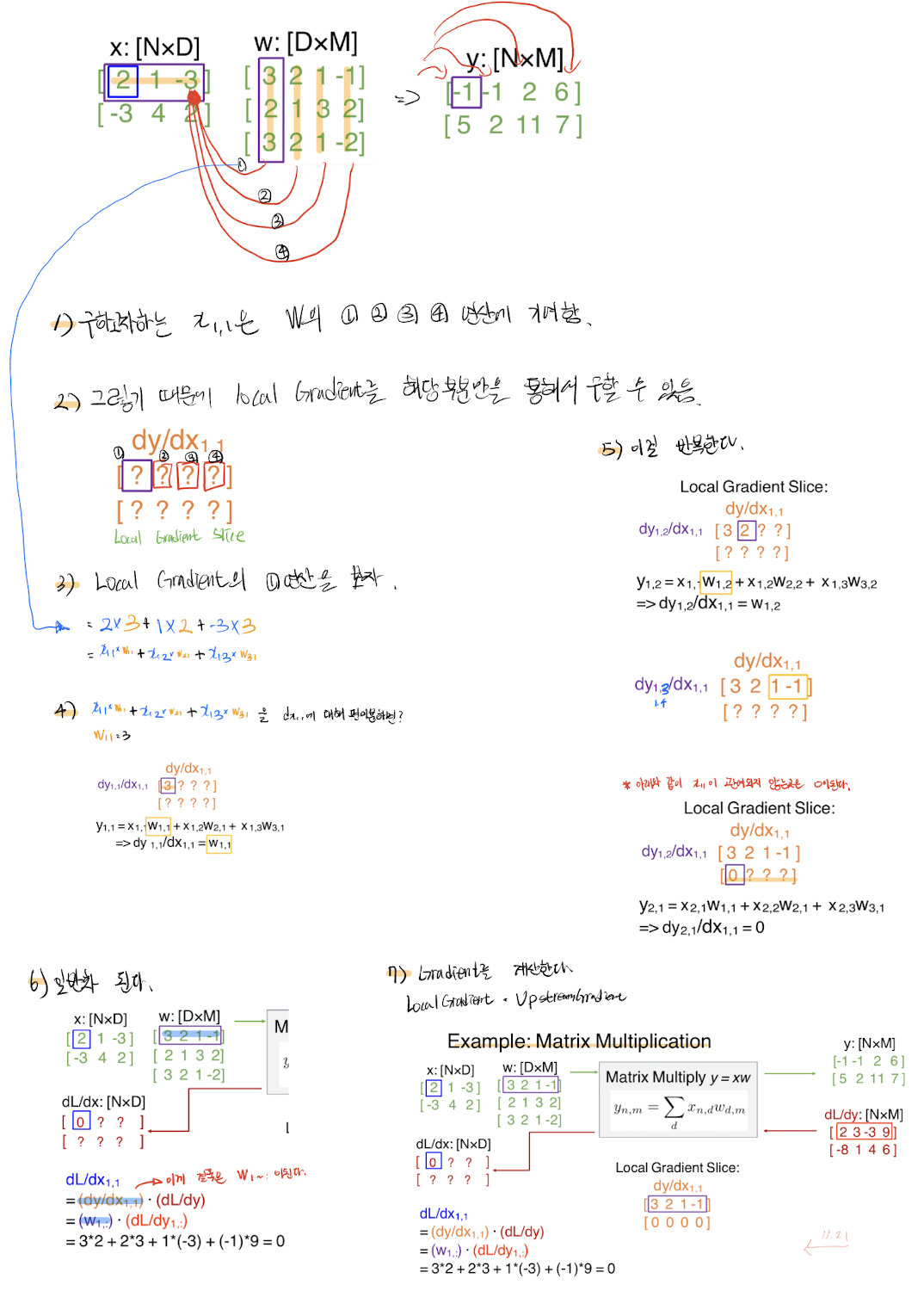
## 결론

자코비안을 쓰지 않고 구할 수 있기 때문에, 메모리를 훨씬 적게 사용 할 수 있다.
![[컴퓨터비전#15/11-21] 행렬(텐서)or벡터의 역전파 과정, 자코비안,Local Gradient Slice, Batch Normalization](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FldS4Q%2FbtrRRu3asP4%2FAAAAAAAAAAAAAAAAAAAAAFRRR-2x3kTx0yDviWawWVluiE8-tU2520Aq96tKkuNX%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3D%252BCdrrDvjYviHfCzM%252BZqS1WPlhI0%253D)