[컴퓨터비전#11/10-31] L1놈과 L2놈을 이용한 Regularization(정규화)

[컴퓨터비전#10/10-09] 로지스틱 회귀 손실함수, 이진 크로스엔트로피 미분하여 경사하강법 도출,

본 포스팅은 2022-10-31(월), 국민대학교 김장호교수님의 컴퓨터 비전 수업을 통해 배운내용을 정리하기 위한 게시글입니다.

---

# 시작하기 전

 시험기간이 있는동안에는 정리글을 쓰지 못했다. 시험공부때문에 시간이 나지 않았는데, 다중 분류와 DNN에 대해서 간단히 배웠었다. 다시 하나씩 정리를 시작해 보도록 하자. 이번시간에는 Regularization에 대해서 배웠다. 

 

# Neural Networks & Weight

 DNN을 배우면서, 일반적인 선형모델에서 벗어나 몇개의 Layer를 쌓는 형태를 공부했었다. 그리고 이 과정에서 단순 선형결합이 아닌, 비선형 결합을 통해서 Layer를 쌓았다. 선형 결합을 하게 되면 Layer를 쌓는 의미가 없어진다. 

 이러한 Layer층의 분리는 각 hidden-Layer에서 특징을 추출하는 의미를 지닌다고 했다.

 위와 같이 Layer를 쌓는 과정에서 가중치(Weight)가 늘어나는 것을 볼 수 있다. 이렇게 Layer를 겹겹이 쌓게 된다면 Weight는 당연히 증가하게 될 것이다.

 Depth가 깊어질수록 Weight가 늘어난다. 여기서는 W1,W2,W3,W4,W5,W6만큼의 Weight가 추가 될 것이다. Weight가 많아진다면 모델의 표현력이 증가한다. 여기까지만 듣는다면 당연히 좋다는 생각이 들 수 있다. 그만큼 정교하게 분류할 수 있다는 뜻이기 때문이다.

## Overfitting

 그러나 이렇게 모델의 표현력이 증가한다는 것은 즉, 오버피팅을 유발함을 알 수 있다. 앞선 인공지능시간과 컴퓨터비전 초창기에 공부했던거와 같이 모델이 training-data-set에 지나치게 편중 된다. 좋은 모델이라 함은 training-data가 아닌 test-data를 잘 맞추어야 한다.

 즉 우리의 모델은 일반화(generalize)된 성능을 가지지 못한다. 결국 모델이 일반화된 성능을 보장 할 수 있도록 학습해야하며, 그렇게 하기 위해서는 Weight를 일반화가 가능하도록 조절 해야 한다. 오버피팅(Overfitting)을 막기 위해서 추가적인 어떠한 장치가 필요하다는 것이다. 

 우리가 사용하던 일반적인 손실함수(Loss-function)은 training-set을 최적화 시켰다. 그렇기에 이 손실함수가 최적화 된다는 뜻은 현재 training-set에 최적화 된다는 뜻이다. 우리가 원하는 건 test-set에서도 최적화가 된 일반화된 것이다. 

 

# Regularization(정규화)

 오버피팅을 방지하기 위해서 어떠한 제한을 걸어줘야 한다. 이를 regularizer라고 한다. 손실함수에 추가적인 장치를 달아 Weight가 너무 커지지 않게 조절해주는 역할을 한다. 

 

오버피팅은 Weight가 커질때 발생한다.

 Weight가 [w1, w2, w3], X가 [x1, x2, x3]가 존재한다고 할때, w1가 w3의 값이 w2의 값에 비해 매우 크다고 생각해보자. 그럴 경우에는 w2x2에 대한 변화에 반응을 보이지 않을 것이다. 그렇기 때문에 Weight를 너무 커지지 않게 조절해줄 필요가 있다. 여러 방법이 있지만 이번 수업에서는 L1,L2를 통한 Regularization에 대해서 배웠다. 

 Weight가 너무 커지면 Weight를 낮추어 주면 될 것이다. 이것을 손실함수에 적용한다면 아래와 같다.

 어려워 보이지만 사실은 별 개념이 아니다. 먼저 손실함수를 Data Loss 부분과 Regularization부분으로 나누어 생각해보자. Data Loss부분은 우리가 여태까지 공부해왔던거와 같이 training-data에 대한 손실값을 나타낼 것이다. 현재 내가 구한 Weight의 값으로 모델을 돌렸을때 실제 정답값과 차이나는 오답값이 많을 수록 loss값이 커질 것이다. 그렇다면 Weight값은 이 Loss을 낮추기 위한 방법으로 다시 Weight값을 갱신 할 것이다.

 여기에 Regulariaztion부분을 추가해준다. 이것은 Weight(가중치)들을 어떠한 방식으로 더한 값들이 될 텐데, 중요한건, Weight값이 커지면 이 Regularization값들또한 커진다. 그렇다면 Loss 함수( L(W) )의 값도 커진다. 그러면 Loss값을 낮추기 위해서 Weight를 갱신할 것이다. 그렇다면 이렇게 갱신되는 값들은 Weight값들이 낮아지게 설정 될 것이다. 이렇게 Regulariaztion을 추가해줌으로써 Weight가 너무 커지지 않게 조절 할 수 있다. 하이퍼마라메타를 줌으로써 이 강도를 따로 설정해줄 수 있다.

 이렇게 Regulariaztion을 해주는 방법에는 위에서 말한대로 L1놈과 L2놈을 활용하는 방법이 있다.

[인공지능#5/09-28] 선형대수(벡터,행렬,분해,놈,선형결합..)

 

# L2놈

 L2놈은 제곱에 루트를 씌워준 것이다. 그러나 루트를 씌워 계산을 복잡하게 할 필요는 없다. 루트는 scale을 결정할텐데 결국 이 scale은 우리가 설정해주는 하이퍼 파라메타로 다시 정의 되기 때문이다. 제곱해주는 대상은 Weight이다.

위에서 본 것 처럼, 손실함수를 만들때, Regularization-Loss를 L2놈의 방식으로 추가 시켜 주면 된다. 하이퍼파라메타(람다)가 scale을 결정해준다 했다. 이것을 시각화 해서 봐보면 아래와 같다.

먼저 Regularization을 통해서 일반화 되는 모델을 볼 수 있다. 우리가 설정해주는 하이퍼 파라메타(람다)가 클수록(0.001 -> 0.1) 손실함수를 계산할때 큰 영향을 줄 것이다. 작을 수록 미미한 영향을 줄 것이기 때문에 모델의 자유도는 클때에 비해서 더 높다.

 

## 경사하강법을 이용하기 위한 미분

 경사하강법을 이용해서 Weight값을 갱신하는 과정을 통해서 최적화된 Weight를 얻을 수 있었다. 손실함수의 미분 정보를 통해서 알 수 있었다. 우리는 Regularization-Loss가 추가된 새로운 손실함수를 정의했기 때문에 L2놈일때 미분 한다면 어떻게 되는지 살펴보자.

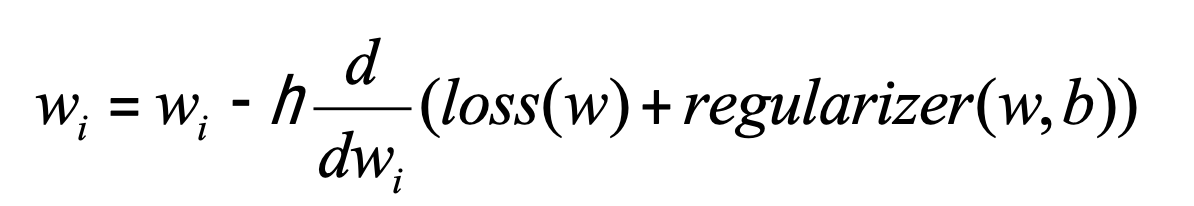
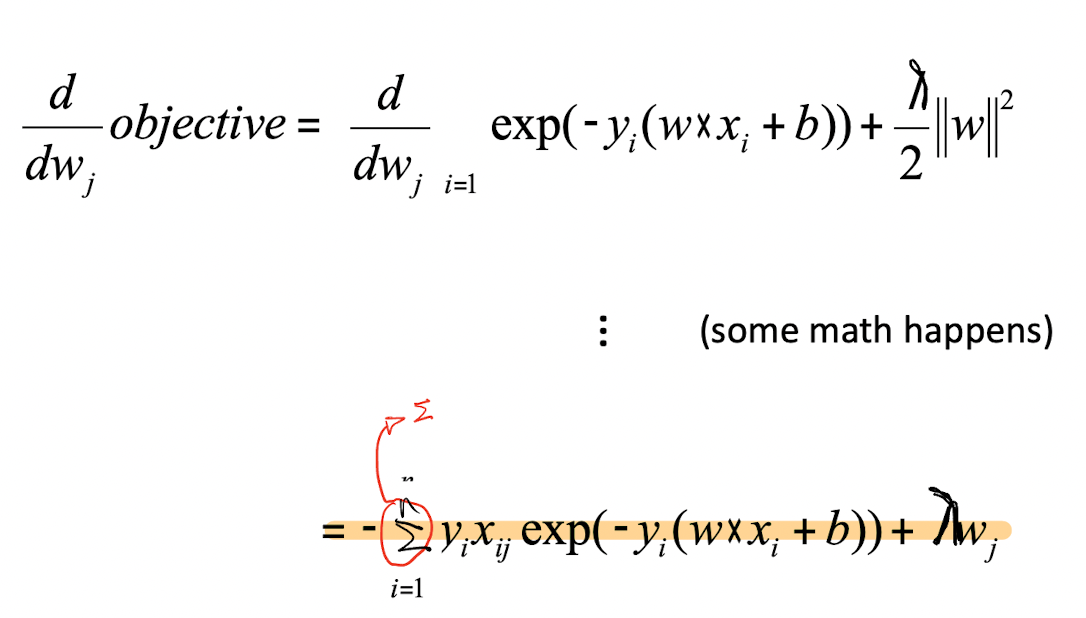
이렇게 미분의 결과를 통해 가중치 갱신을 할 수 있을 것이다.

 

바로 뒤이어 나올 L1놈도 위와 유사한 결과를 얻는다.

 

# L1놈

 

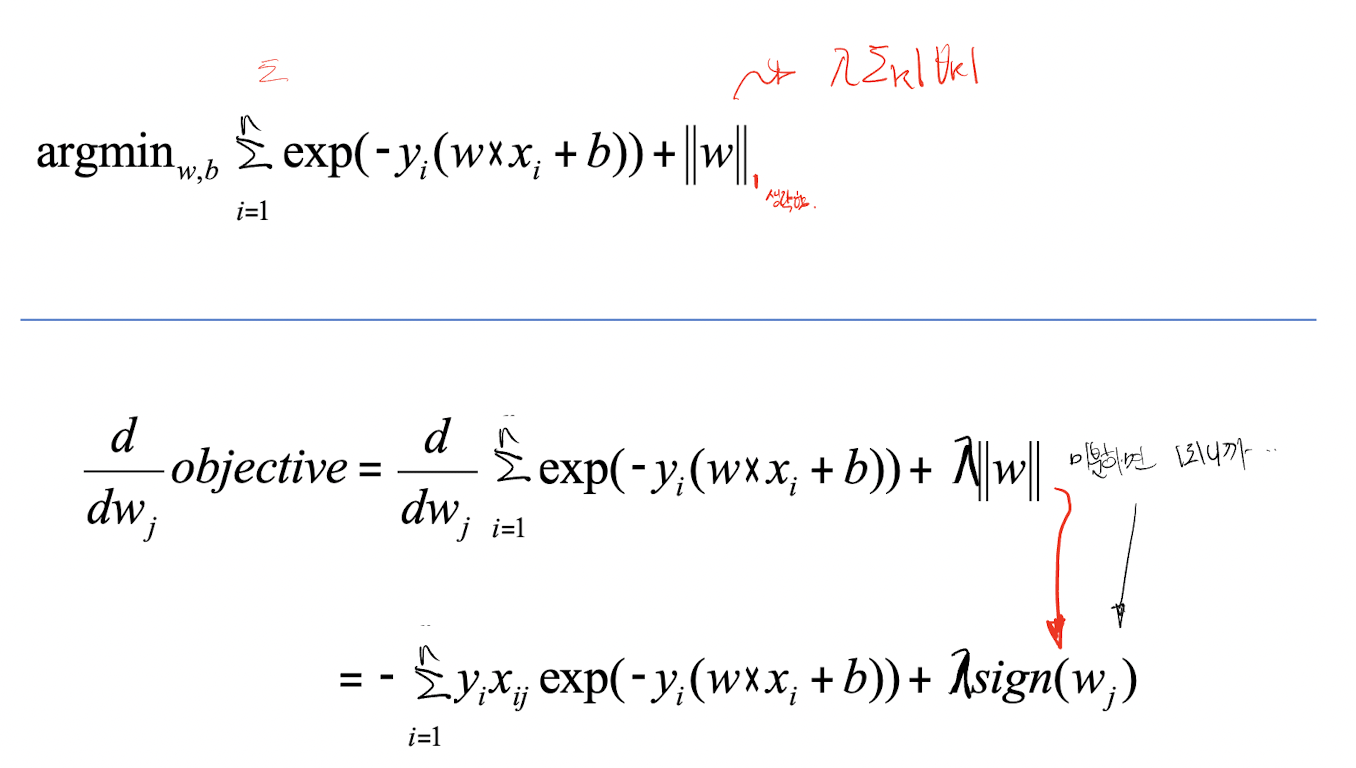
다만 L1놈과 L2놈의 차이가 있다면, 미분이 주는 결과다. L2놈은 비례한 결과를 가지겠지만, L1상수배 차이가 된다. L2놈과 L1놈이 가지는 특성을 생각해보면 쉽게 이해가 될 것이다.