[인공지능#4/09-21] 학습모델(검증, k-교차검증)선택, 규제(데이터 증대, 가중치 패널티), 인공지능
[인공지능#3/09-19] 기계학습 훈련과정, 오버피팅(overfitting)과 언더피팅(underfitting), 편향(bias)과 변 [인공지능#2/09-14] 특징공간, 차원의 저주, 기계학습의 전반적 개요 및 목적함수의 의미와 훈련과 [
devforyou.tistory.com
본 포스팅은 2022-09-28(수), 국민대학교 이재구 교수님의 인공지능 수업을 통해 배운내용을 정리하기 위해 작성하는 게시글입니다.
# 선형대수와 인공지능

선형대수를 통해 데이터를 쉽게 다룰 수 있고, 데이터 분석에 필요한 배경을 제공해준다.
수 -> 벡터 -> 행렬 -> 텐서와 같이 차원이 확장됨에따라 형태가 나타난다.
IRIS데이터에는 꽃받침의 길이, 꽃받침의 너비, 꽃잎의 길이, 꽃잎의 너비가 각각 5.1, 3.5, 1.4, 0.2로 나타난다 했을때 다음과 같이 표현 할 수 있다.
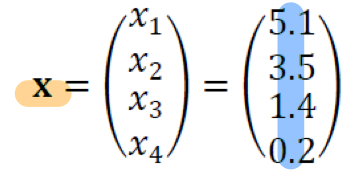
# 벡터

벡터를 이루는 데이터의 개수가 n개이면 n차원 벡터라고 표현한다. IRIS데이터의 예시에서 x는 R^4차원이라고 볼 수 있을 것이다.
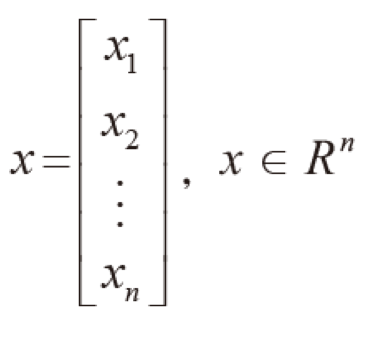
놈(norm)은 벡터의 크기(magnutude)또는 길이(length)를 나타낸다. 다음챕터에서 자세히 다루도록하고, 놈은 벡터의 크기이다라는 사실을 알고 있자.
# 행렬
여러개의 벡터를 담고 있다. 행과 열이 존재한다. 또한 열을 Feature라고 볼 수 있다. 아래 그림을 살펴보자.

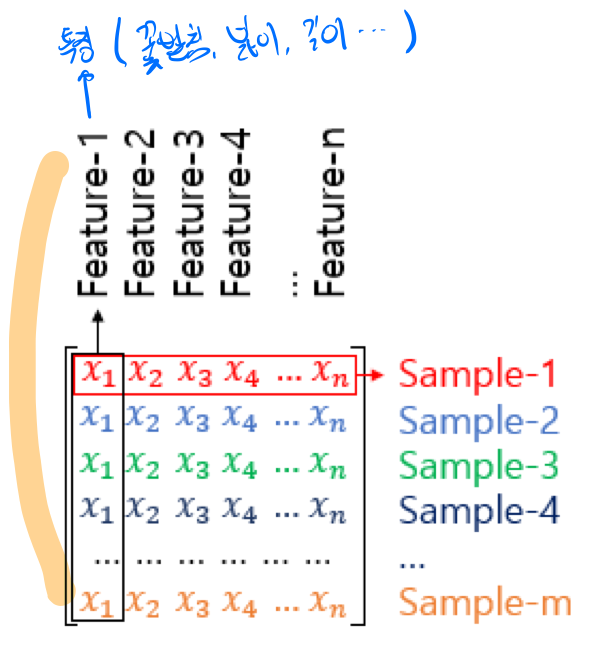
행렬로 정리된 까닭에 열벡터와 행벡터를 통해서 원하는 데이터를 쉽게 다룰 수 있다. 150개의 IRIS데이터를 Feature별로 분류되어 행렬로 표현 할 수 있다.
# 벡터간 거리

벡터의 거리를 3가지 방법으로 표현이 가능하다.


## 1차놈 (L1 : Manhattan distance)


1차놈의 형태는 다음과 같다. (우이미지 참고)맨해튼 거리는 절대값의 합을 구하기 때문에 거리가 1,2,3인 경우를 각각 표시해보면 왼쪽이미지와 같게 된다.
## 2차놈 (L2 : Euclidean distance)


2차놈은 (우이미지 참고) 제곱의 루트의 값이 되고 이를 표현해보면 원의 반지름과 같다. 그래서 거리가 1,2,3을 표현해보면 왼쪽이미지와 같아진다.
## 놈의 사용
모델에 제약을 걸어 overfitting을 방지해주기 위해서 사용한다. 가중치 혹은 매개변수를 작게 조절하는 것이다. 손실함수에 놈을 더해줌으로써 규제방법을 이용한 제약을 걸 수 있다.
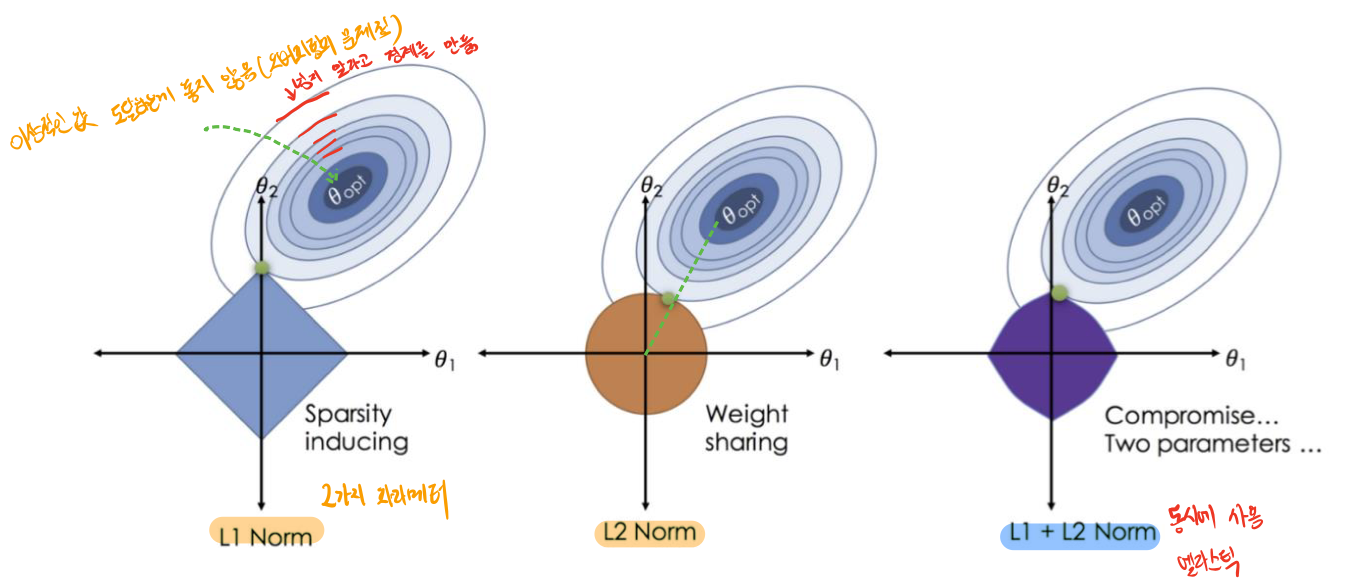
즉, 놈이 이상적인 값에 도달하지 않도록 하기위해서이다. 이상적인 값에 도달한다는것은 훈련집합에 너무 편중된 나머지 오버피팅(overfitting)을 유발할 수 있기에, 놈을 사용해서 경계를 만들어 도달하지 못하도록 하는 것이다.
# 벡터의 곱셈
## 스칼라와 벡터의 곱

벡터의 각요소의 스칼라값을 곱해준다.
## 벡터 내적
벡터를 내적하면 cos세터 의 값을 구할 수 있다. 세터를 통해서 두 사잇각을 알고 이를 통해서 두사잇각을 알 수 있다. 결국 두 벡터의 방향의 유사도를 알 수 있는 것이다.

내적을 통해서 스칼라값을 알 수 있다. 두벡터의 내적의 값을 구했다.

두 벡터의 크기의 곱을 내적의 값에 나누어준다면 구하고자하는 cos세타를 구할 수 있다.

## 벡터의 외적
벡터를 외적하면 두벡터의 법선 벡터가 나온다. 이 법선벡터의 절대값(크기)를 구하면 두벡터의 볼륨임을 알 수 있다.

# 선형 결합
백터의 스칼라값을 곱하거나 더해줌과 같은 연산을 통해서 새로운 벡터 공간을 형성하는 것이다.
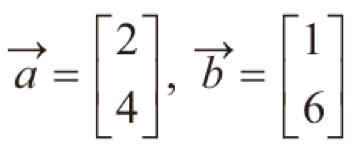

이 두 벡터의 선형 연산을 통해 새로운 벡터를 얻었다. 이를 좌표공간에 표시해보면 아래와같이 표현 됨을 알 수 있다.

## 선형독립과 선형 종속

벡터집합에 대해 임의의 계수를 곱해줬을때, 그 계수가 모두 0이어야만 0을 만족하는 것을 선형 독립이라고 한다. 선형독립일 경우에는 면이나 공간등을 표현할 수 있게 된다.
## 공간과 기저(base)

공간을 생성하는 일종의 뼈대가 된다. 선형독립인 경우에 기저를 형성할 수 있다. 2차원 평면상의 예를들어, 선형종속인 경우 아무리 두벡터를 통해 늘리고 줄여 선형결합을 해도 선분밖에 만들지 못한다. 이렇게 공간을 생성할때 최소한 필요한 선형독립 벡터의 집합을 기저라고 한다.
# 랭크(rank)
임의의 행렬에서 열들로 생성될 수 있는 벡터 공간의 차원이다. 3개의 벡터로 만들 수 있는 차원이 2차원이라면, rank는 2가 되는 것이다.

1열과 2열의 행렬을 합치면 3열의 행렬을 만들 수 있다. 1열과 2열의 경우만 선형독립이기때문에 만들수 있는것은 면이 될 것이다. 그렇게 때문에 rank는 2이다.

1열,2열,4열의 행렬은 서로종속이다. 3번째 행렬(0,0)을 제외하면 1,2,4열의 행렬로는 아무리 선형결합을해도 선은 만들수 있을 것이다. 그렇기 때문에 rank는 1이다.
# 행렬식(determinant)

역행렬을 판단해준다. det(A) = 0이면 행렬A는 역행렬을 가지지 않고, 그렇지 않다면 역행렬을 가진다.
# 정부호행렬

# 고유값과 고유벡터



행렬은 벡터를 변환시켜주는 연산자이다. 행렬을 통해 새로운 벡터를 만들 수 있는데, 이렇게 벡터의 행렬을 곱해도, 방향은 바뀌지 않고 크기만 바뀌는 것을 고유벡터라고 한다.
# 행렬 고유분해
# 행렬 특잇값 분해
# 참고
선형독립 선형종속
[선형대수] 선형독립(linearly independent), 선형종속(linearly dependent)
이번 포스팅에서는 선형독립 혹은 1차 독립(linearly independent)과 선형종속 혹은 1차 종속(linearly dependent)에 대해서 알아보겠습니다. 선형독립 혹은 1차 독립 (linearly independent) 개념은 나중에 이어..
rfriend.tistory.com
고유벡터
고윳값과 고유벡터 - 공돌이의 수학정리노트
angeloyeo.github.io
'•Compter Science > Artificial Intelligence' 카테고리의 다른 글
| [인공지능#7/10-05] 정보이론과 엔트로피, 크로스엔트로피, KL-Divergence, 경사하강법 (0) | 2022.10.08 |
|---|---|
| [인공지능#6/10-03] 확률과 조건부 확률, 베이지 정리를 이용한 IRIS 추정 (0) | 2022.10.08 |
| [인공지능#4/09-21] 학습모델(검증, k-교차검증)선택, 규제(데이터 증대, 가중치 패널티), 인공지능 기본수학 (1) | 2022.09.25 |
| [인공지능#3/09-19] 기계학습 훈련과정, 오버피팅(overfitting)과 언더피팅(underfitting), 편향(bias)과 변동(variance) (0) | 2022.09.20 |
| [인공지능#2/09-14] 특징공간, 차원의 저주, 기계학습의 전반적 개요 및 목적함수의 의미와 훈련과정 (0) | 2022.09.18 |
![[인공지능#5/09-28] 선형대수(벡터,행렬,분해,놈,선형결합..)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2F3VT9I%2FbtrNwEvdV2D%2FAAAAAAAAAAAAAAAAAAAAAHaiI5JcW2Uz2crRGF6VOmdGHRcYZc8-8OcpL54rhSZp%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DfmilFJqGQggwGYHAjrUR8m1BkEE%253D)