[인공지능#5/09-28] 선형대수(벡터,행렬,분해,놈,선형결합..)
[인공지능#4/09-21] 학습모델(검증, k-교차검증)선택, 규제(데이터 증대, 가중치 패널티), 인공지능 [인공지능#3/09-19] 기계학습 훈련과정, 오버피팅(overfitting)과 언더피팅(underfitting), 편향(bias)과 변 [.
devforyou.tistory.com
본 포스팅은 2022-10-03(월), 국민대학교 이재구 교수님의 인공지능 수업을 통해 배운내용을 정리하기 위해 작성하는 게시글입니다.
# 시작하며
#5, #6, #7에 걸쳐서 인공지능에서 많이 활용되는 수학 행렬-벡터 / 확률 / 정보이론 및 최적화 에대해서 배우고 있다.
# 확률 실험
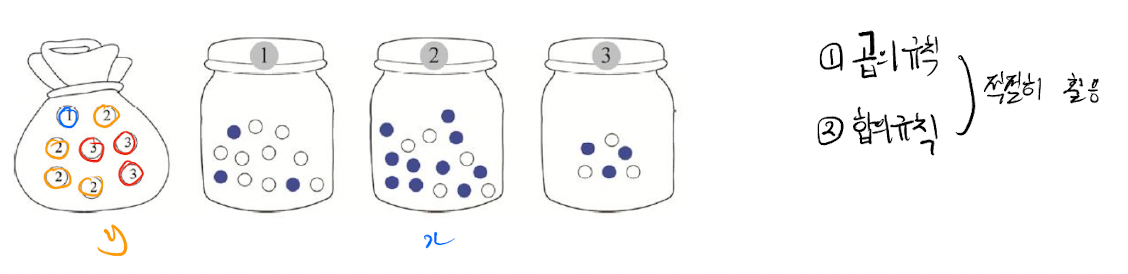
그림과 같이 주머니 한개와, 3개의 병이 있다고 생각해보자. 우린 주머니에서 뽑아 나온 숫자에 해당하는 병에서 공을 뽑을 것이다. 병에는 하얀공과 파랑공 두가지가 있다. 조건부 확률에대해서 공부하기전에 합의규칙을 잠깐 되새겨보자. 주머니에서의 확률변수를 y, 병에서의 확률변수를 x라하고 각각의 정의역은 y = { 1, 2, 3 } , x = { 파랑, 하얀} 이 된다.
## 합의 규칙
만약 주머니에서 1번공과 2번공을 뽑는 확률 을 구하면 어떻게 될까. P(y=1)와 P(y=2)의 합으로 표현 할 수 있다. 두 사건은 동시에 일어나는 사건이 아니기 때문이다. 간단히 1/8 + 4/8 = 5/8 이라는 답을 내릴 수 있다.
## 조건부 확률 , 결합확률
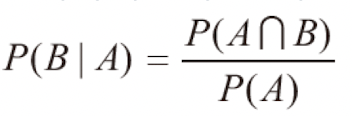
어떤 사건 A가 일어났다는 조건하에 다른 사건 B가 일어나는 확률이다. 예를 들어, 주머니에서 1번공이 나왔을때 파랑공이 나올 확률과 같이 조건이 붙는다.
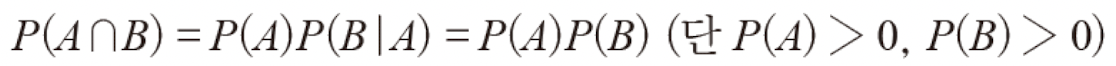
그러나 이 두사건이 서로에게 연관이 없을수도 있다. 즉 A가 일어나든 말든 B의 확률은 같다는 뜻이다.

여튼 이렇게 몇개의 확률이 결합되어 나타나내느 형태를 결합확률이라고 하며 P(y=1, x=하얀)과 같이 표현하며, 두사건이 종속관계인지 독립관계인지 잘 알아야 한다.
## 카드는 1번, 공은 하얀공일 확률
P(y=1, x=하얀) == P(1,하얀)일 확률을 구해보자. 이 사건은 서로 종속인 사건이기때문에 계산에 유의해야한다. 조건부 확률 공식에 의하면 P(A n B) = P(B | A) * P(A)의 형태로 나타내졌다. 이를 통해서 해당 결합확률은, (1번이뽑혔을때하얀공이 뽑힐 확률) * (1번이 뽑힐확률)의 꼴로 나타 낼 수 있다.
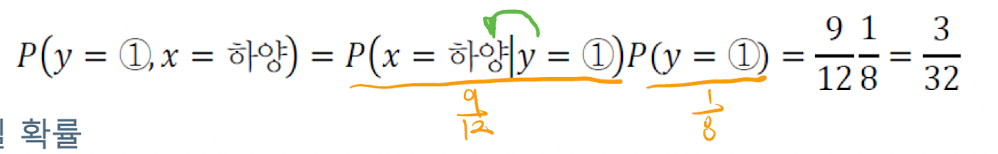
## 하얀 공이 뽑힐 확률?
하얀 공이 뽑힐 확률은 어떻게 될까, P( y, x= 하양)인 경우이다. 하양공이 뽑힐 모든 결합확률은 아래와 같이 3가지 일 것이다.

그렇다면 이 세가지 확률의 합이 하얀공이 뽑힐 확률이 될 것이다. 이를 즉 특정사건 x(하양공이 나올 확률)에 주목하여 계산 하는 것을 아래와 같이 표현 할 수 있다.

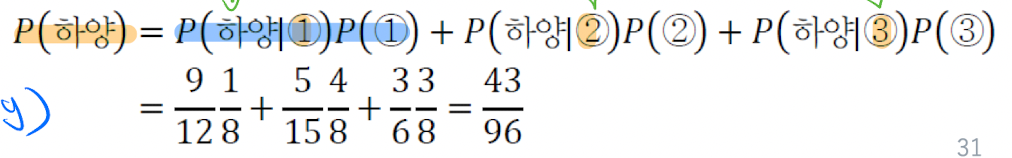
## 베이지 정리

일어나지 않았거나 불확실한 사건에 대해서는 베이지안 확률을 구할 수 있다. 여기서 사후확률, 우도확률, 사전확률, 주변우도라는 개념이 등장한다. 우도는(likelihood)로써 우리의 데이터로 이미 알 수있는 상황이다. 사후 확률은 직접적으로 알 수 없다. 이런 사후 확률을 구하기 위해서 우도와 사전확률을 사용한다. 이 데이터들은 우리가 이미 알 수 있는 데이터이기 때문이다.
### 하얀공이 나왔을때 이 공은 어디에서 나왔는가?
이는 어떤 사건이 만들어 놓은 상황에서, 그 사건이 일어난 후 앞으로 일어나게 될 다른 사건의 가능성을 구하는 것을 말한다. 즉, 기존 사건들의 확률(사전 확률)을 알고 있다면, 어떤 사건 이후의 각 원인들의 조건부 확률을 알 수 있다는 것이다.
출처 : 나무위키
일반적으로 하얀공이 나왔을때 이공은 어디(주머니)에서 나왔는가에 대한 직접적인 추론은 불가능하다. 왜냐하면 주머니에서 먼저 공을 뽑고 이를 통해서 하얀공을 뽑기 때문이다. 베이지정리를 이용함으로써 이러한 추론이 가능하다.
먼저 베이지 정리의 식을 다시 정리해보자.
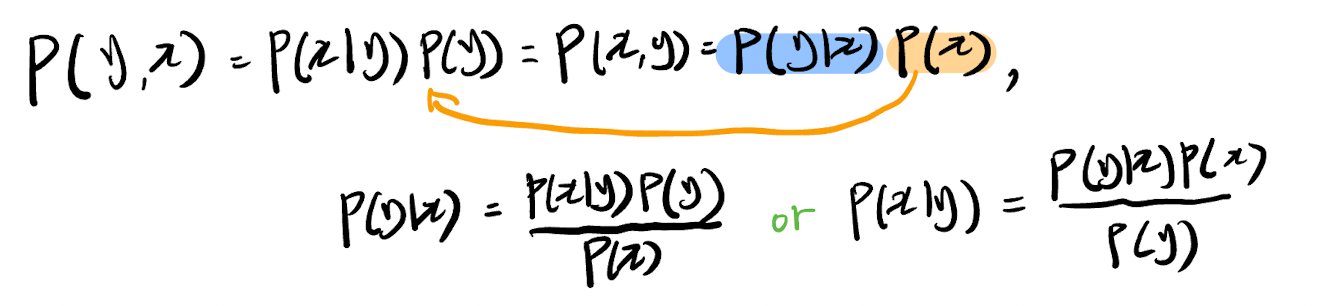

즉 베이지 정리를 통해 조건을 다시 정리해보면, 사후확률에 대한 계산을 할 수 있게 된다. 우린 우도와 사전확률을 알 수 있기 때문에 구해진 값들에서 argMax를 찾을 수 있다.
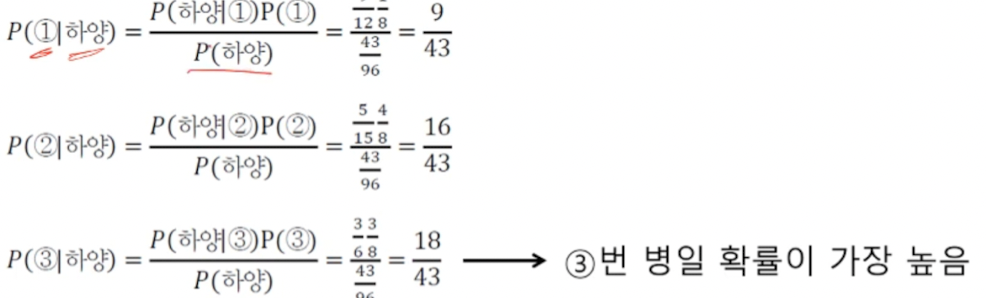
결국 직접 구하지 못하는 사후확률에 대한 추론이 가능해졌다. IRIS 데이터를 통해서 조금 와닿게 이해해보자.
### IRIS 데이터

IRIS데이터에는 4가지의 특징 데이터가 있었다. x = { 꽃받침의 길이, 꽃받침의 너비, 꽃잎의 길이, 꽃잎의 너비 } 이 특징벡터에 대한 결과로는 y = { setosa, versicolor, virginica } 이라고 맵핑된다. 즉 우리가 어떤 꽃의 특징벡터(x)를 토대로 이것은 어느 IRIS인지를 찾아 내야 했다.

쉽게말해 x라는 데이터가 setosa일 확률, x라는 데이터가 versicolor일 확률, x라는 데이터가 virgincia일 확률 중 가장 높은 확률을 지니는(argMax)를 찾는 과정이다. 근데 이 사후 확률을 직접 구하는 것은 불가능하다. 그냥 데이터가 X일때 Y(IRIS)를 알 수 있다면 굳이 구할 필요도 없을 것이다. 우리는 우리가 가진 데이터들로 이 추정을 해내야 한다. 그렇기 때문에 베이지정리를 사용하여 우도확률과 사전확률을 사용 할 수 있다.
이러한 P( setosa | x )일때의 확률을 구하기 위해서 베이지정리를 활용해 식을 바꾸어 본다면, 아래와 같다.

즉 이렇게 3가지의 값중에서 가장 큰 값을 가지는 것을 선택하면 된다.

'•Compter Science > Artificial Intelligence' 카테고리의 다른 글
| [인공지능#8/10-12] 인공신경망, 퍼셉트론 개념 (0) | 2022.10.13 |
|---|---|
| [인공지능#7/10-05] 정보이론과 엔트로피, 크로스엔트로피, KL-Divergence, 경사하강법 (0) | 2022.10.08 |
| [인공지능#5/09-28] 선형대수(벡터,행렬,분해,놈,선형결합..) (0) | 2022.10.01 |
| [인공지능#4/09-21] 학습모델(검증, k-교차검증)선택, 규제(데이터 증대, 가중치 패널티), 인공지능 기본수학 (1) | 2022.09.25 |
| [인공지능#3/09-19] 기계학습 훈련과정, 오버피팅(overfitting)과 언더피팅(underfitting), 편향(bias)과 변동(variance) (0) | 2022.09.20 |
![[인공지능#6/10-03] 확률과 조건부 확률, 베이지 정리를 이용한 IRIS 추정](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FlPWuN%2FbtrN5E3a2f8%2FAAAAAAAAAAAAAAAAAAAAAN1KIIi-FnxUkNYXu-Vc9CkUkvZoNR7bmIuJx1fb0g2i%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3De4sYEEQPdroLfvW8fvjfxfdTanU%253D)