[인공지능#7/10-05] 정보이론과 엔트로피, 크로스엔트로피, KL-Divergence, 경사하강법
[인공지능#6/10-03] devforyou.tistory.com 본 포스팅은 2022-10-05(수), 국민대학교 이재구 교수님의 인공지능 수업을 통해 배운내용을 정리하기 위해 작성하는 게시글입니다. # 시작하기 전 해당일(10-05)에
devforyou.tistory.com
본 포스팅은 2022-10-12(수), 국민대학교 이재구 교수님의 인공지능 수업을 통해 배운내용을 정리하기 위해 작성하는 게시글입니다.
# 시작하며
이번 주차부터 새로운 3챕터에 들어왔다. 1단원에서 기계학습에 관한 주요개념들을 배웠고 2단원에서는 기계학습에 필요한 수학적 개념들을 다뤘다. 이제 시작하는 3단원에서는 인공신경망과 퍼셉트론, 다층 퍼셉트론, 오류 역전파에 대해서 배운다.
# 인공 신경망
인간의 뇌를 구성하는 "뉴런"과 유사한 형태를 구현하여 인공 신경망을 구성 할 수 없을까라는 문제에 대한 해결방법이다.

뉴런은 뇌에서 가장 작은 정보처리 단위이다. 컴퓨터 과학과 뇌과학이 합쳐져 인공신경망을 구현한다. 즉 뇌의 정보처리 과정을 모방한다는 것이다.
이러한 인공신경망을 퍼셉트론이라고 하며 XOR문제를 해결 할 수 없다는 한계에 부딪혀 한때 주춤하다가 다층 퍼셉트론을 제안하고, GPU와 방대한 데이터의 시대가 열리면서 주류 기술로 자리 매김 했다.
## 종류
- 전방 신경망, 순환신경망
- 결정론적 신경망, 확률론적 신경망
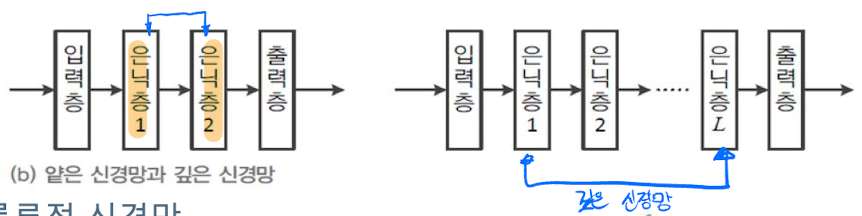
인공 신경망에는 입력층과 출력층으로 나뉜다. 입력층은 흔히 생각하는 데이터가 입력 되는 과정이며, 일련의 과정을 거쳐 출력층으로 데이터가 출력 된다. 그리고 이 사이의 은닉층이 존재하여 우리가 앞에서 배웠던 w가 결정되는 구간이 존재한다. 이러한 은닉층이 적으면 얕은 신경망, 많으면 깊은 신경망이 된다.
# 퍼셉트론

우리 뇌의 뉴런과 퍼셉트론을 살펴보자. 우리가 어떠한 것에 의해서 뉴런이 입력값을 받으면 우리의 경험들에 의해서 결정된 가중치의 값들이 입력값에 연산되고 결과물이 연관된 그 다음 뉴런으로 전달되는 과정을 거치면서 뇌과 동작한다.
퍼셉트론에도 어떠한 입력 데이터가 들어오면, 학습을 통해 결정된 weight값의 가중치가 더해지고 값이 결정된다. 이후 활성함수로 one-hot-encoding과 같이 표현될 것이다.
## 가중치
입력층에는 항상 1인 가중치가 들어간다. 왜냐하면 h(x) = wx + b에서 b는 이러한 가중치 역할을 한다. 이 값은 우리가 활성함수를 거칠때 임계점의 역할을 해준다. (c)의 경우 0을 기점으로 -1과 1의 부분이 나뉜것 처럼 말이다.
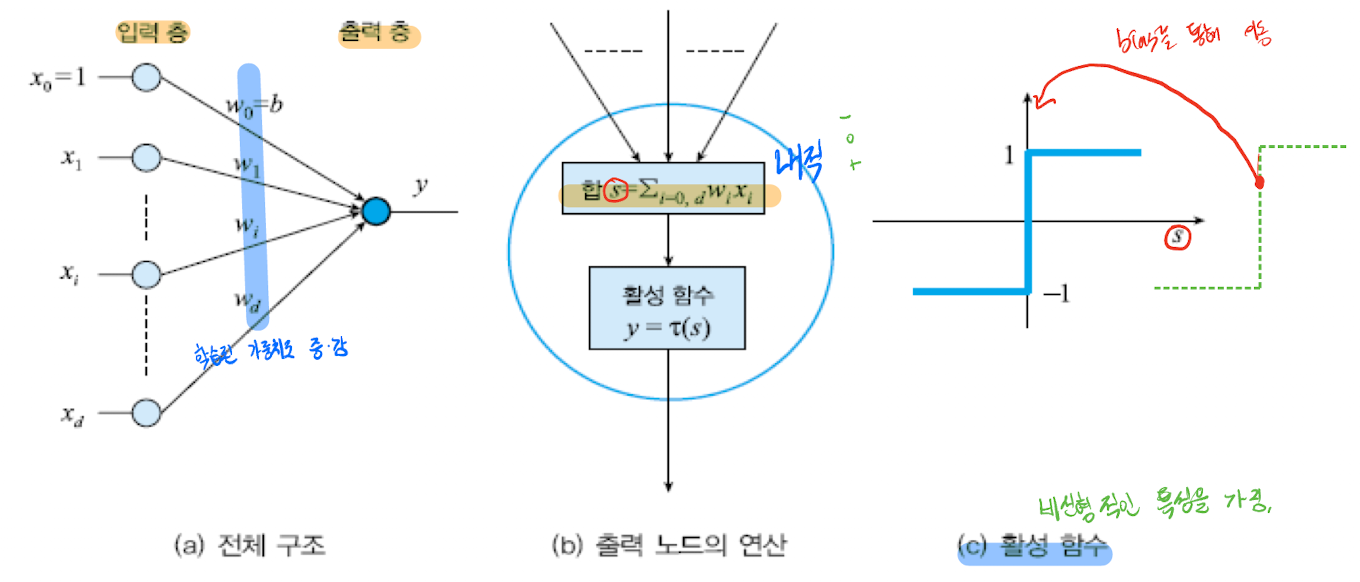
가중치가 1인 이유는 행렬의 곱연산을 생각하면 쉽다.

위와 같이 연산이 되기 때문이다. 그래서 가중치(b)를 행렬안에 넣어줄수도 있고 행렬 밖으로 빼서 표현 할 수 도 있다.

## 연산 방법

뉴런과 퍼셉트론을 비교한 이미지에서 볼 수 있듯이, 우린 최종 결과값을 만들어 내기전에 경험으로 얻어낸 가중치값을 입력데이터와 곱하여 더해준다.

이러한 선형연산을 거친 후에, 1과 -1의 형태의 최종 결과가 나올 수 있게 활성 함수를 거친다. 즉 아래와 같이 최종 수식이 결정 될 것이다.

## 예시
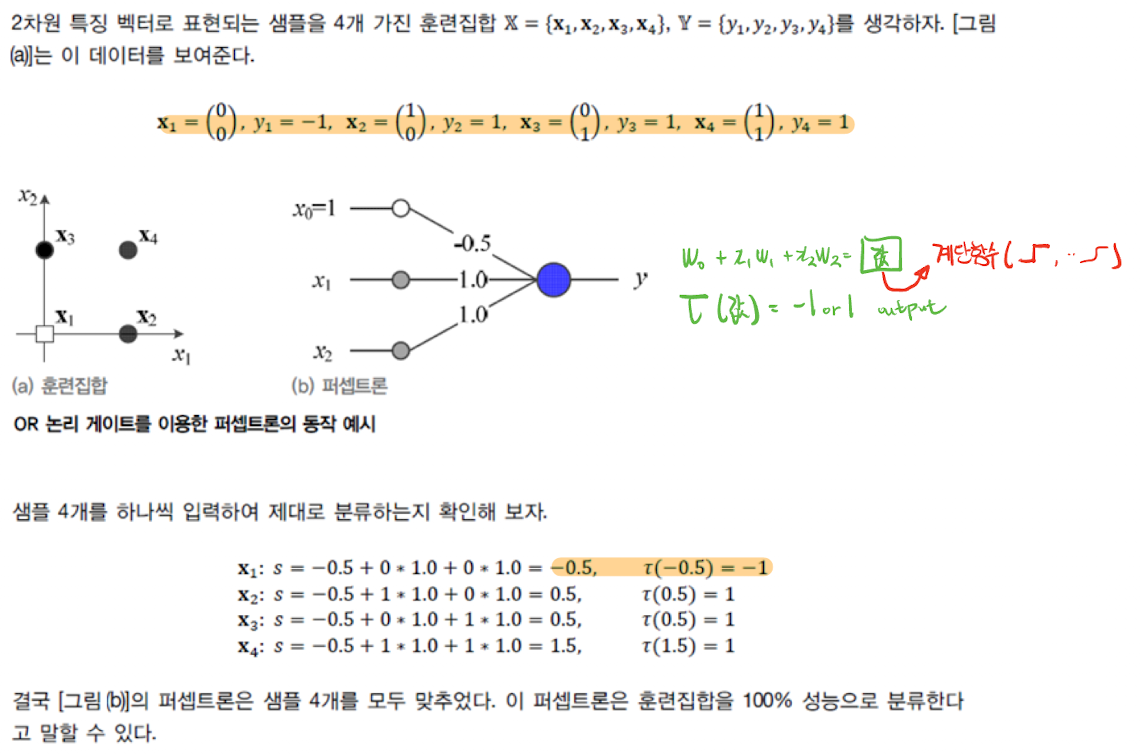
총 입력 데이터는 4개, 각 입력데이터는 특징 벡터이며 두개의 특징(feature)가 있다. 퍼셉트론에 한 입력이 들어올때 두개의 feature에 대해서 처리 할 것이다. 가중치의 선형연산이 끝난 후 활성함수(step function)에 값을 넣어 최종 결과 값을 확인해보자.
# 퍼셉트론의 목적(손실)함수
[컴퓨터비전#10/10-09] 로지스틱 회귀 손실함수, 이진 크로스엔트로피 미분하여 경사하강법 도출,
[컴퓨터비전#9/10-05] Classification, Linear Regression, Logistic Regression, sigmoid [컴퓨터비전#8/10-03] 경사하강법(Gradient Descent)과 Learning Late, Stochastic Gradient Descent [컴퓨터비전#7/09-2..
devforyou.tistory.com
분류기를 만들기 위해서는 첫째로 가설(모델)을 설정해야 하고, 그 분류기에 맞는 손실함수를 새로 정의해야 한다. 그리고 경사하강법과 같은 방법으로 W를 최소화 하는 최적화 방법을 수행해야 한다. 컴퓨터 비전단원에어서 먼저 배웠듯이, 이진 분류를 하기 위해서 시그모이드 활성함수를 사용했을때, 손실함수로 MSE를 사용하면 local minimum지점이 생기기 때문에 적합하지 않았고, 이진크로스엔트로피라는 손실함수를 사용했다.
목적 함수를 정의하기 위해서는 아래의 조건을 충족시켜야 한다.

즉, 손실함수는 항상 양수의 값만을 가져야 하며, 최적의 지점 W가 결정 될때 손실함수의 값은 0, 에러가 클 수록 손실함수의 값또한 커져야 한다. 아래 손실함수는 위 조건을 충족시킨다.
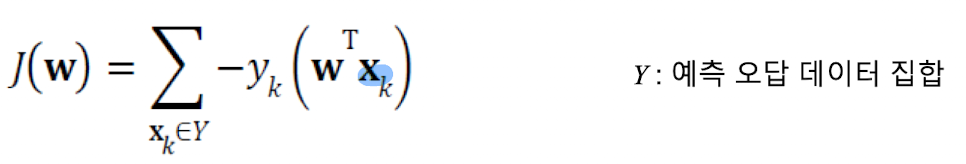
Y는 예측 오답 데이터 집합이다. 그렇기 때문에 정답(1) * 오답(-1)은 항상 오답이 될 수 밖에 없다.
## 경사도 계산
위 조건을 충족시키기 때문에 경사하강법을 통해 미분을 이용한 최적화 방법을 수행 할 수 있다.

목적함수를 우리가 최적화하고싶은 매개변수 w_i에 대해서 편미분한다. 편미분은 우리가 볼 값에 대해서만 관심을 가진다. 결국 모든 손실함수가 최적화가 되는 지점이라 함은 모든 w에 대해서 만족해야 하기 때문에 이러한 과정을 매개변수마다 거쳐서 최적의 w들의 지점을 찾아야 할 것이다.
'•Compter Science > Artificial Intelligence' 카테고리의 다른 글
| [인공지능#10/11-07] CNN의 구조 및 특징, 패딩, 보폭(Stride), Pooling (0) | 2022.11.09 |
|---|---|
| [인공지능#9/10-31] 깊은 신경망(DNN)과 CNN 맛보기 (0) | 2022.10.31 |
| [인공지능#7/10-05] 정보이론과 엔트로피, 크로스엔트로피, KL-Divergence, 경사하강법 (0) | 2022.10.08 |
| [인공지능#6/10-03] 확률과 조건부 확률, 베이지 정리를 이용한 IRIS 추정 (0) | 2022.10.08 |
| [인공지능#5/09-28] 선형대수(벡터,행렬,분해,놈,선형결합..) (0) | 2022.10.01 |
![[인공지능#8/10-12] 인공신경망, 퍼셉트론 개념](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FvbXXE%2FbtrOscxGyBl%2FAAAAAAAAAAAAAAAAAAAAAB18fPnen8Ig8-gezxbcgBejmxYq3-32MKQvQ-fJaiBK%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3D0bJ051iWtU5nXi2t5Kzz5s6fhQI%253D)