[컴퓨터비전#9/10-05] Classification, Linear Regression, Logistic Regression, sigmoid
[컴퓨터비전#8/10-03] 경사하강법(Gradient Descent)과 Learning Late, Stochastic Gradient Descent [컴퓨터비전#7/09-28] Linear Regression, 벡터화, feature map [컴퓨터비전#6/09-26] 기계학습의 종류와 개념..
devforyou.tistory.com
본 포스팅은 2022-10-09(월), 국민대학교 김장호교수님의 컴퓨터 비전 수업을 통해 배운내용을 정리하기 위한 게시글입니다.
# 이전강의
이전 강의에서 binary classification의 문제를 해결하기 위해 로지스틱 회귀방법을 사용해야하는 이유를 배웠다. 간단히 다시 정리해보면, Linear regression으로 classification문제를 해결하려고 하면 튀는 이상값이 생긴다면 내가 설정한 임계점대로 분류해도 예상과 다른 분류결과가 나옴을 알 수 있었다.

이러한 문제는 Linear가 0~1사이의 값이 아닌 그 이상의 값도 나올수 있기 때문에 생겨버렸다. 이문제를 해결하기 위해서 y의 범주를 0~1사이로 제한하기 위해 sigmoid함수를 사용했다.

그렇게 새로운 모델에 대한 가설을 세웠다면, 손실함수를 검증해야한다. Sigmoid함수로 얻은 로지스틱함수에서 손실함수를 그대로 사용한다면 Local minimum문제에 빠지게 됐다. 그래서 정답과 근접하면 낮은 손실함수값을 정답가 멀어지면 높은 손실함수의 값을 반환하는 손실함수를 찾았다.

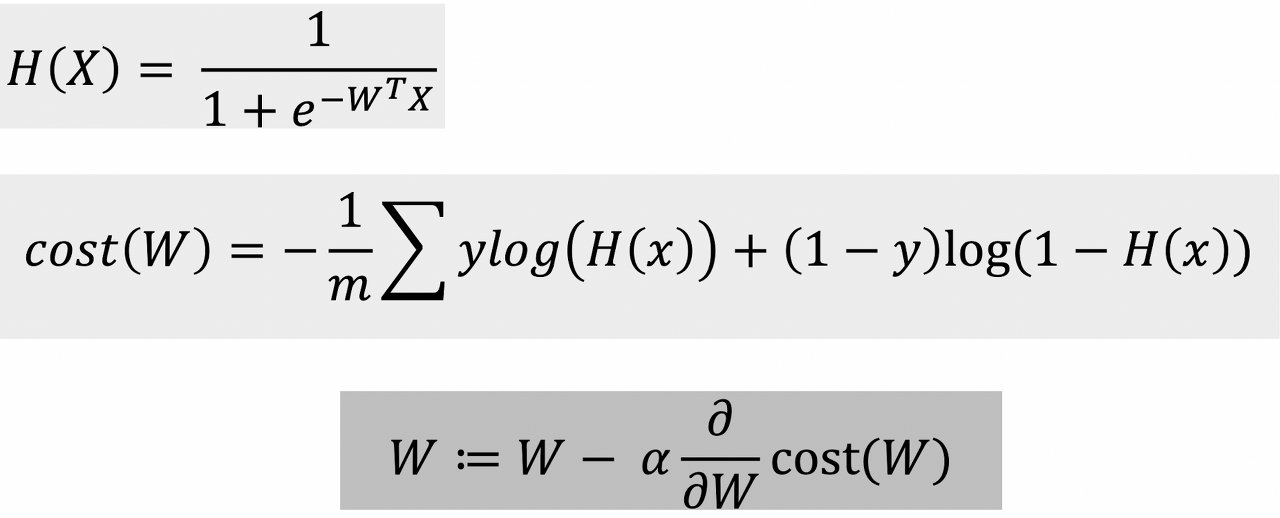
cost(W)식을 정리하면 이진 교차(크로스) 엔트로피가 된다.
결국 이진 교차(크로스) 엔트로피는 로지스틱회귀의 손실함수가 된다는 것이다.
이번시간에는 이 손실함수를 통해서 경사하강법을 어떻게 진행하는지 알아보도록 하자.
# 경사하강법
[컴퓨터비전#8/10-03] 경사하강법(Gradient Descent)과 Learning Late, Stochastic Gradient Descent
[컴퓨터비전#7/09-28] Linear Regression, 벡터화, feature map [컴퓨터비전#6/09-26] 기계학습의 종류와 개념, 손실함수, 손실함수와 파라메타 [컴퓨터비전#5/09-21] 그레디언트(엣지방향,강도), 소벨마스크 엣
devforyou.tistory.com
우리는 경사하강법을 어떻게 구했는지 다시금 생각해보자. 경사하강법은 손실함수의 최적화를 통해 가장 작은 손실함수의 값을 찾아내는 것이다. 그렇게 하기 위해서는 손실함수의 미분값을 통해서 얻어낸 함수가 증가하는 방향의 역방향으로 하여 Learing Rate값을 조절해주어 그 간극을 좁혀 나갔다.

그렇다면 로지스틱회귀의 손실함수를 미분하여야 한다. 근데 이 미분과정이 꽤나 까다롭다. 어떻게 미분을 할 수 있는지 살펴보자.
## 이진 교차(크로스) 엔트로피 미분

즉 이 미분결과를 통해서 경사하강법을 이용할 수 있게 된다.
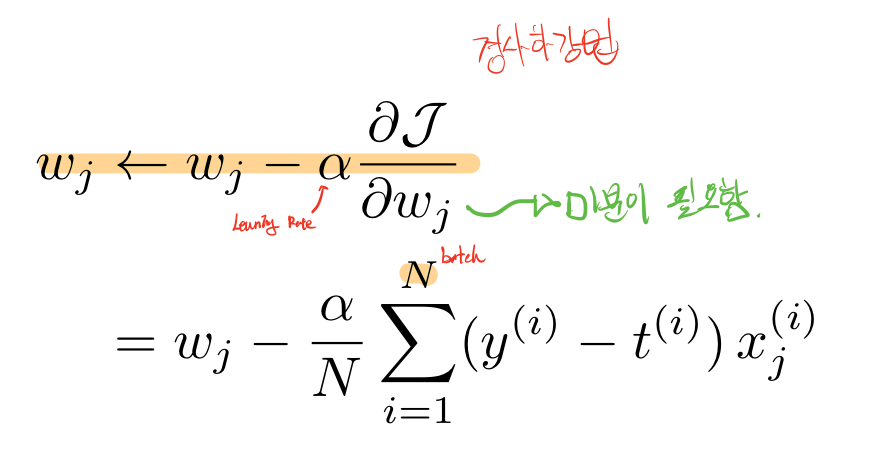
# 소프트맥스(Softmax) 활성함수

Multiclass Classification의 경우 discrete set이 벡터로 표현되며 2개가 아닌 K개의 값을 가질 수 있다. 우리의 최종 출력 결과는 { 철수, 영희, 호준, 민수 } 4가지의 다중 분류에서 호준이라고 분류된다면 { 0, 0, 1, 0 }의 형태로 출력되어야 한다는 것이다. 즉 이것을 One hot Encoder라고 하는데 Softmax함수를 통해서 모든값이 0~1사이, 전체합이 1로 확률정규화를 시켜준다.
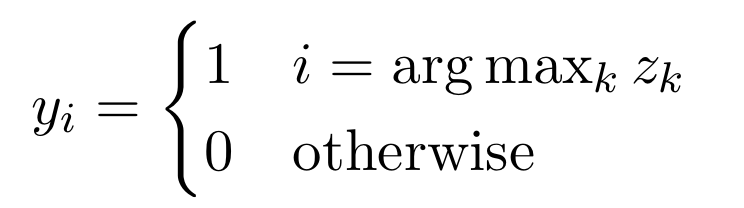

![[컴퓨터비전#10/10-09] 로지스틱 회귀 손실함수, 이진 크로스엔트로피 미분하여 경사하강법 도출, 소프트맥스 함수, one-hot-encoding](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbiL0P8%2FbtrN79oCKVu%2FAAAAAAAAAAAAAAAAAAAAAKz8hDkMzw9rx2IWnSOVjkzEdPLudZB-q9Mz44lTLTYK%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DLqHYu1Dk4MulQ9mrxfitYu%252B5OsU%253D)