[컴퓨터비전#7/09-28] Linear Regression, 벡터화, feature map

[컴퓨터비전#6/09-26] 기계학습의 종류와 개념, 손실함수, 손실함수와 파라메타

본 포스팅은 2022-09-28(수), 국민대학교 김장호교수님의 컴퓨터 비전 수업을 통해 배운내용을 정리하기 위해 작성하는 게시글입니다.

---

# 시작하며

함수 f*의 진리값(최적)의 함수가 존재한다. 우리의 목표는 input데이터 Z로부터 대략적은 함수를 만들어 진리의 f*에 근접하게 만드는 것이다. 그러나 f*를 정확히 알 수 없기 때문에 어렵다. 

Linear Regression에서 이 일련의 과정들은 3단계로 나누어 볼 수 있다.

교사 학습의 방법이 되기 때문에 (x,y)데이터를 수집하는 과정과, 최적의 손실함수를 가지는 파라메타 베타를 찾아내는 과정, 이를 최적하여 모델을 만들어내는 과정이다.

 

# Linear Regression

즉, 수식으로 정리해보면 위와 같다. 결국 궁극적인 목표는 손실함수의 최소값을 가지게하는 파라메타를 찾는 것이다. 선형회귀 이기때문에 Linear functions을 모델로 택할 것이다. 

 

# Vectorization

데이터를 처리할때는 벡터화 과정을 거치는 것이 좋다. 만일 CPU를 통해 연산하게 되면 아래와 같이 직렬적으로 단계를 밟아가면서 처리를 해야한다. 

 

그러나 아래와 같이 벡터화를 거쳐 GPU를 통해 연산을 하게 되면 병렬적으로 데이터를 처리할 수 있다. 쉽게 예를 들자면, 100개의 연산이 한번에 일어나 100개의 결과값이 한번에 나오게 되는 것이다.

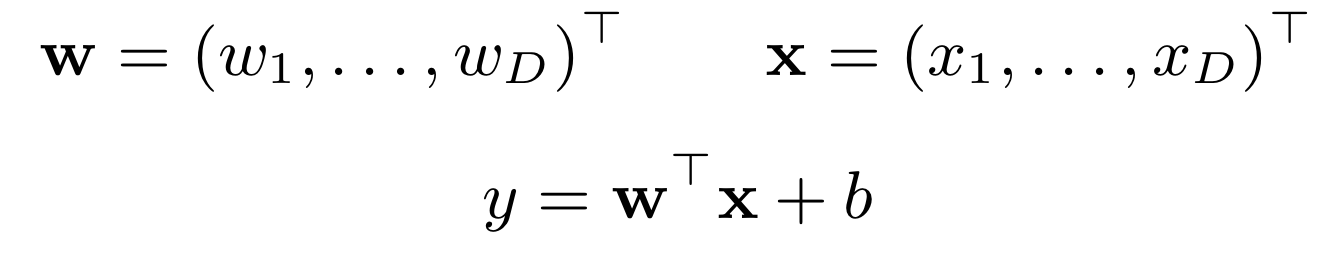
GPU는 이렇듯 행렬곱에 최적화 되어 있다.

 

# Quadratic Function

Quadratic Function을 직역하면 2차함수라는 의미를 가진다. 2차함수의 모양을 되새겨 보면서 아래의 예제를 살펴보자.

위와 같은 데이터들의 분포가 있다는 가정하에, 1차함수로써 이 데이터를 표현하면 어떻게 될까? 아무리 기울기를 바꾸어보아도 곡선의 모양에 최적화 시킬 수 없을 것이다. 즉 1차원으로써는 최적의 값을 찾을 수 없다는 뜻이다. 그렇다고 non-linear model을 설정하면 해결 될 것 같지만, 앞서 배웠듯 non-linear은 처리하기 까다롭다. 그래서 feature map라는 개념이 등장한다.

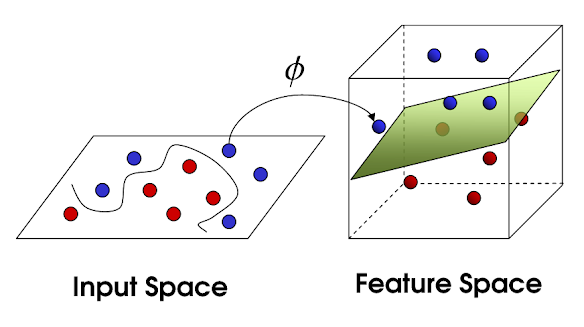
이러한 input Space를 linear model이 해결할 수 있는 feature space Φ(x)로 만들어 해결한다. 이러한 feature space를 만들어주는 함수가 feature map이다. 

이렇게 Φ(x)를 사용하게 되면, input x에 대해서 값이 나오듯이 Φ(x)라는 함수를 이용해서 feature를 만들어 준 것이다. 

그렇게 모델에 파라메타가 추가되면 아래와 같이 표현이 가능해진다.

그렇게 최종적으로 원하는 표현이 가능해진다.

일련의 과정을 정리해보면 아래와 같다.

 

 

# 그렇다면 lots of features를 사용하는게 좋지 않을까?

차원이 커지기 때문에 당연히 모델의 자유도가 높아져 표현범위가 넓어진다. 그러나, 오버피팅의 문제점을 가진다. 인공지능시간에 공부했듯이, 테스트데이터만을 잘 맞추고, 정작 맞춰야하는 새로운 데이터들에 맞출 수 없게 된다. 변동성(variable)을 가지게 된다. 

위와 같이, 오히려 낮은 차원의 모델이 new data에 대해서 오차값이 더 작을 수 있다는 말이다. 

 

그렇다면 모델이 작으면 또 좋은건 아니다, underfitting(과소적합)의 문제를 가지기 때문이다. bias가 커지기 때문에 그냥 잘 맞추지 못한다. 

언더피팅과 오버피팅에 대해서 재밌는 예제를 들어 주셨다. 변동성과 편향성을 영점사격할때 탄착군으로 설명해주셨다.

맞춰야하는 정중앙 과적에 대해서, overfitting은 들쑥날쑥하는 변동성을 지니고, underfitting은 중심과는 멀어지지만 그래도 뭉쳐있다. 이게 편향성(bias)이다. 

 

## 그렇다면 어떤걸 써야하나?

웃기게도 적당한 모델을 선정해야한다. 많이써보면 경험적으로 직관적으로 알 수 있다고 하셨다. 언더피팅이 난다면 모델의 크기를 키워주고, 오버피팅이 난다면 모델의 크기를 줄여주는 과정을 거쳐야 한다.

 

# 끝내며

Feature Map을 활용해서 바뀐게 결국 2차원이기 때문에 선형이 아니지 않냐에 대해서 질문을 드렸는데, 이또한 좌표계에 2축으로 표현한다면 선형 모양이라고 하셨다. 근데 이해가 잘 되지 않았다..

 

# 참고

Linear regression with Feature Map 참고자료

[머신러닝/딥러닝] 11-1. Kernel의 이해와 종류

 

Linear 참고자료

[머신러닝/딥러닝] 1. Linear Models for Regression