[컴퓨터비전#4/09-19] 엣지 검출, 엣지 검출을 위한 미분 활용, 이미지에서의 미분 개념
[컴퓨터비전#3/09-16] 필터링( 메디안, 평균, 가우시안), 동차좌표와 동차행렬 [컴퓨터비전#2/09-14] 히스토그램, 히스토그램 평활화, 점연산(선형,비선형,디졸브),영역연산(상관, 본 포스팅은 2022-09-14
devforyou.tistory.com
본 포스팅은 2022-09-21(수), 국민대학교 김장호교수님의 컴퓨터 비전 수업을 통해 배운내용을 정리하기 위해 작성하는 게시글입니다.
# 시작하며
저번시간에는 미분을 통해서 엣지인 지점을 어떻게 찾을 수 있는지, 이를 마스크를 통해서 계산하는 방법에 대해서 배웠다. 배운 내용을 간단히 요약 해보며 시작하겠다.
영상(=이미지)에서 엣지(edge)는 픽셀 값이 급격하게 바뀌는 부분을 뜻했다. 우리는 함수로써 이미지를 표현 할 수 있기에, 미분을 이용해서 이를 해결 할 수 있었다. 미분에서는 극한값을 사용했지만, 우린 여기서 델타x의 경우를 한픽셀 단위 즉 최소픽셀 단위인 "1"을 이용할 수 있었다.

미분해서 얻은 y값은 원래 함수에서의 기울기의 크기를 나타낸다. 즉 0보다 크면 해당 구간에서 양의 기울기를, 0보다 작다면 음의 기울기를 0이라면 원래함수에서는 기울기가 0(증가하거나 감소하지 않음)이라는 뜻이다. f'(x)에서의 값이 0보다 훨씬 크거나 훨씬 작은위치를 찾는다면, f(x)에서 값이 급격하게 변화하고 있다고 유추해볼 수 있을 것이다.
## 영상은 2차원 (x,y)이다.

그러나 이렇게 해서 찾는 값들은 한방향에서의 기울기의 변화를 관측하는 것일 것이다. 즉 이미지에는 x,y 두값이 있다. x만을 이용한다면 수평방향의 엣지만 검출 될 것이며, y만 사용한다면 수직방향의 엣지들만을 관측 할 수 있을 것이다. 그래서 이번 강의에는 x,y를 사용하여 어떻게 엣지를 검출 하는가에 대해서 배울 수 있었다.
# 간단한 수학적 용어 정리
편미분과 그래디언트(gradient)라는 용어가 등장해서, 수학을 다 까먹은 나로써 긴가민가 했다. 간단히 정리해보자.
## 편미분
다변수 함수에서 미분할 변수를 제외한 나머지 변수를 상수취급해서 미분하는 것이다.
아래 예를 살펴보면,


x에 대해서 미분하기 때문에 y에 대해서는 그냥 상수취급하여, x^2 -> 2x , xy -> y , y^2 -> 상수로 없어진 것을 알 수 있다.
## 그래디언트(gradient)

그래디언트는 간단히 말해, x축 방향의 미분과 y축방향의 미분을 한꺼번에 벡터로 표현한 것이다. 삼각형을 뒤집어 놓은 꼴로 표기한다.

벡터는 방향과 크기를 지니기 때문에, 이또한 방향과 표기로 표현 할 수 있다.
아크탄제트의 꼴을 취하게되면 방향(각도)가 나온다.
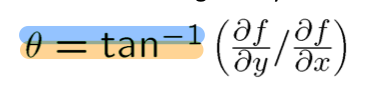
우리가 거리를 구하는 공식과 유사하게 벡터의 크기는 아래와 같이 구할 수 있다.
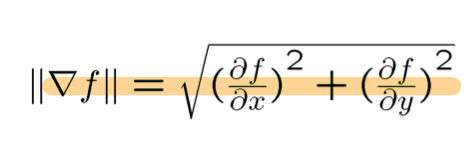
이를 확장해서 생각해보면, 그래디언트는 벡터의 방향은 변화가 가장 큰 방향을 표시하고, 그래디언트 벡터의 크기는 세기(변화율)을 나타내는 척도로써 생각할 수 있게 된다.
# 에지 강도와 에지 방향
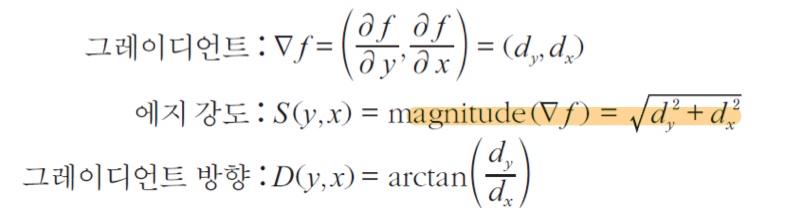
위에서 배운 그래디언트를 사용하여 에지방향이 어떻게 표시되는지 봐보자.

빨간색으로 표시된 선이 그래디언트이다. 그래디언트의 세기는 화살표의 길이, 방향은 화살표가 가르키는 방향이 될 것이다. 이 그레디언트의 수직방향이 엣지 방향이 된다.
## 소벨 마스크를 이용한 엣지 검출


소벨 연산자의 my , mx모두가 주어졌다. 이를 이용해 dy, dx의 편미분을 구해보자.
- dy : my => ( -3 + -2 + 1 ) = -4
- dx : mx => ( -3 + -4 + 8 + 1 ) = 2
이 편미분 값에 아크탄젠트를 해 그래디언트각도를 얻어내면 -63.4도, 그래디언트 강도 4.47이 된다. 이를 그림에 표시하면 빨간선이 나오게 된다. 여기에 90도를 더하면 엣지의 그레디언트가 될 것이다.
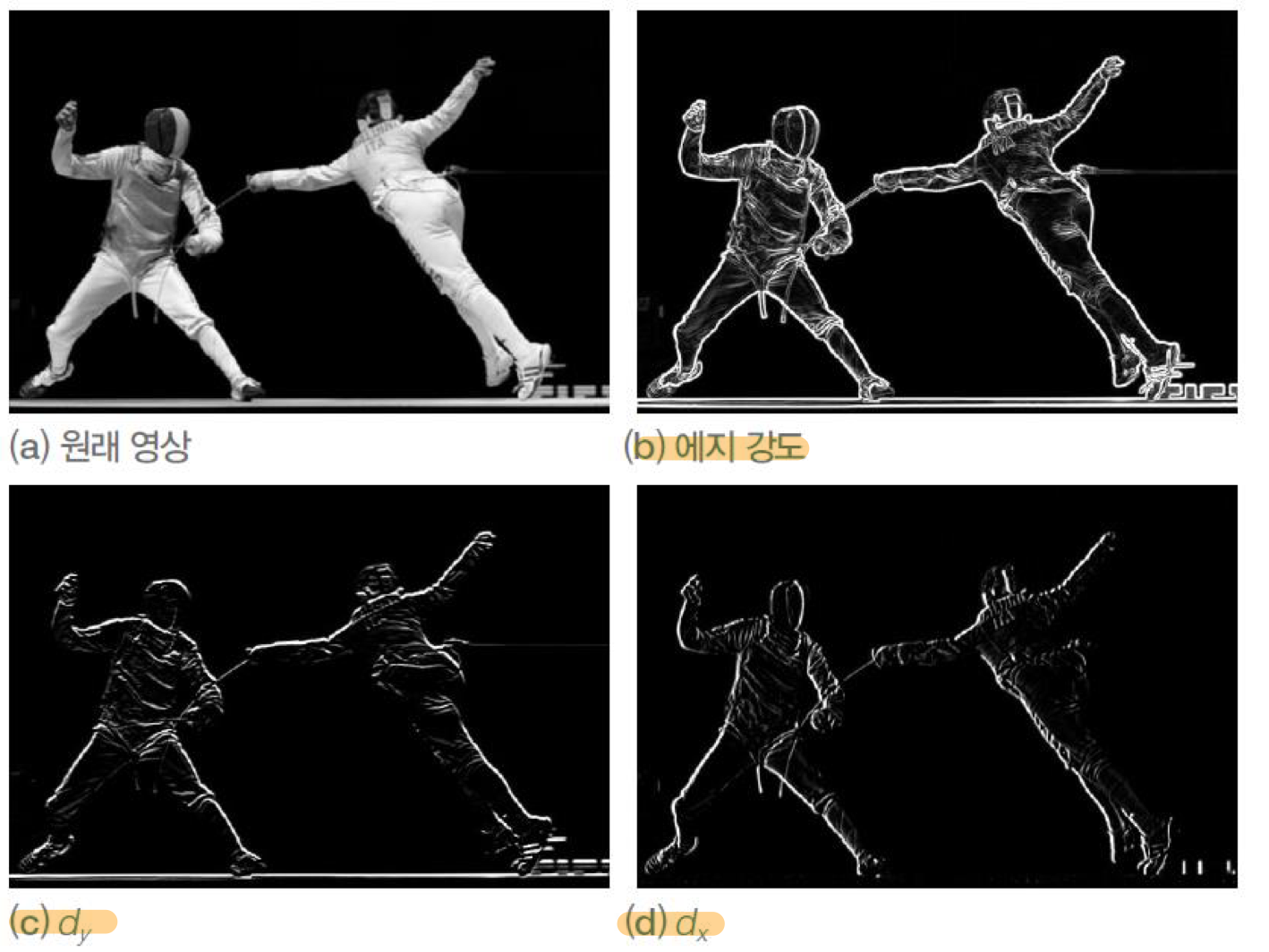
# 엣지는 잡음에 민감하다.
미분은 잡음을 증폭시킨다. 원래영상에 솔트페퍼 잡음(이미지상 9)가 존재한다고 가정해보자.
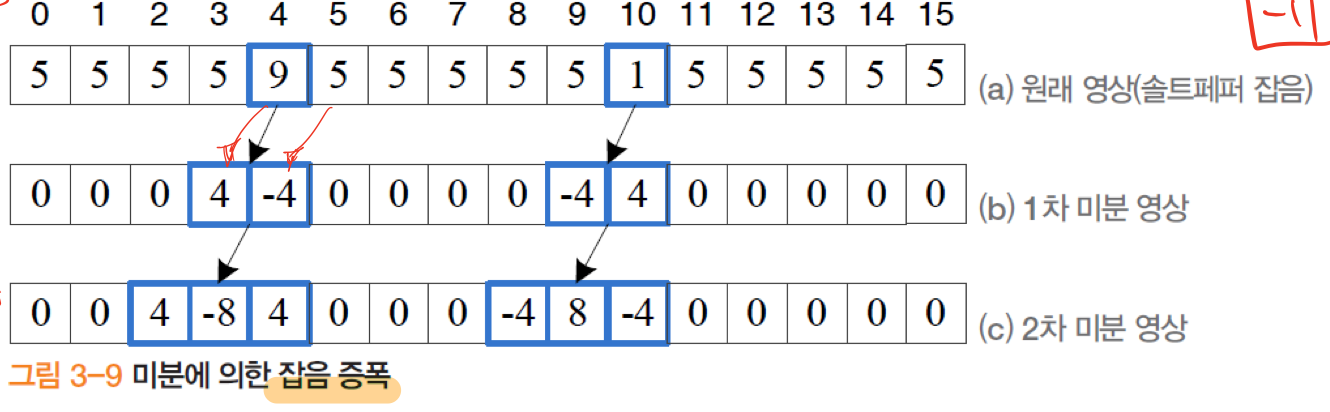
미분을 통해 얻어낸 값은 기울기가 증가, 감소하는지 알 수 있다. 그 증가 감소는 결국 양 옆을 보면서 알 수 있는데, 잡음이 있는 상태로 미분을 하게 되면 양옆을 비교하는 탓에 점점 증폭됨을 알 수 있다.

실제 엣지는 파란 부분이지만, 잡음(노이즈) 때문에 미분된 값을 보게되면 엣지를 찾을 수 없다는 것을 알 수 있다.
# 엣지 검출전에 잡음(노이즈)을 제거하자
이에대한 해결책은 간단하다. 엣지를 검출하기전에 노이즈를 제거하면 된다. 노이즈를 제거하는 필터를 사용하면 된다.
먼저 가우시안필터를 사용해서 노이즈를 제거하는 과정을 살펴보자.


즉, 노이즈제거 -> 미분하여 엣지구하기이다. 근데 우리는 결합법칙이 적용됨을 알 수 있다. 이과정을 줄일 수 있다.
## 개선된 방법(DOG)
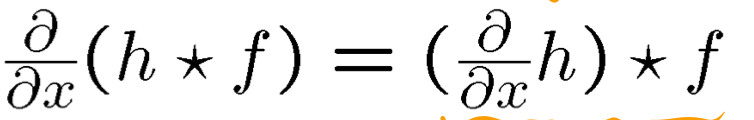
앞서 봤던 원본에 가우시안에 필터를 돌리고 미분하는게 아닌, 가우시안 필터를 미분하고 원본에 그 필터를 돌리면 된다. 결합법칙이 주는 힘으로 번거로운 과정을 줄였다.

이를 DOG필터라고 한다.

## LOG
### Marr-Hildreth 에지 검출 알고리즘

에지를 구하는 알고리즘 중 2차미분을 통해 영교차를 찾에 에지를 검출하는 방법이다. 여기에는 라플라시안 연산자가 사용된다.
라플라시안 연산자, 2차 미분을 구해주는 마스크를 얻을 수 있다.

여기도 똑같이 가우시안으로 스무딩후 라플라시안 연산자를 적용하는 번거로운 과정이 있다. DOG처럼 한과정으로 줄일 수 있다.
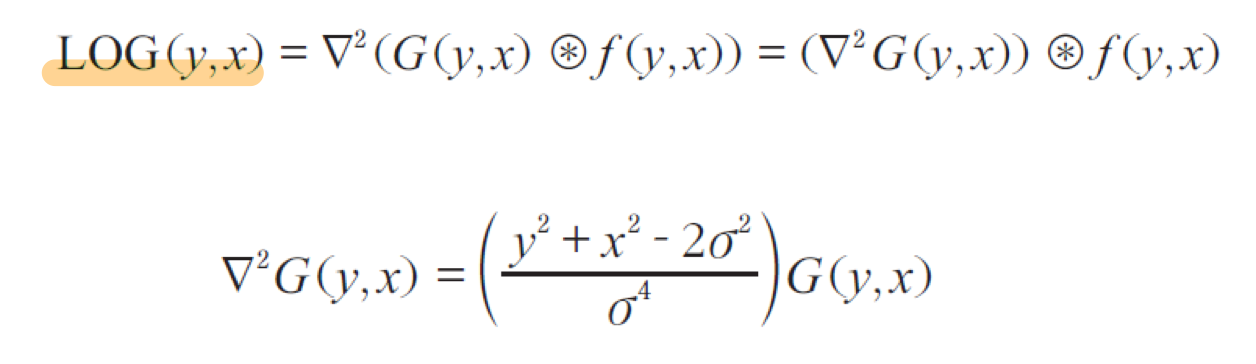
이 의미를 간단히 요약해보면 아래와 같다.

# LOG 필터가 적용된 Marr-Hildreth 알고리즘 사용해보기



우리는 LOG필터가 있기때문에, 가우시안으로 노이즈 제거 -> 2차 미분하기의 과정을 LOG필터를 사용함으로써 한단계로 줄일 수 있다.
Marr-Hildreth의 검출 방법에 따라서, LOG필터로 구한 값들의 북-남, 동-서, 북서-남동 , 복동-남서의 4가지 부호차를 살펴본다. 북-남, 북서-남동이 부호차이가 생기기때문에 1차 조건을 만족하고, 이 부호가 다른 쌍들의 각각의 차가 임계값(T=1)을 만족하기에 해당 부분을 엣지로 검출할 수 있다. 그래서 (b)영교차 검출된 영상에서 엣지라고 표시를 하게 되는 것이다.
# 2D edge detecction filters

'•Compter Science > Computer Vision' 카테고리의 다른 글
| [컴퓨터비전#7/09-28] Linear Regression, 벡터화, feature map (0) | 2022.09.29 |
|---|---|
| [컴퓨터비전#6/09-26] 기계학습의 종류와 개념, 손실함수, 손실함수와 파라메타 (2) | 2022.09.28 |
| [컴퓨터비전#4/09-19] 엣지 검출, 엣지 검출을 위한 미분 활용, 이미지에서의 미분 개념 (1) | 2022.09.20 |
| [컴퓨터비전#3/09-16] 필터링( 메디안, 평균, 가우시안), 동차좌표와 동차행렬 (1) | 2022.09.19 |
| [컴퓨터비전#2/09-14] 히스토그램, 히스토그램 평활화, 점연산(선형,비선형,디졸브),영역연산(상관,컨볼루션) (0) | 2022.09.15 |
![[컴퓨터비전#5/09-21] 그레디언트(엣지방향,강도), 소벨마스크 엣지검출, 엣지 잡음과 DOG & LOG 마스크](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FmkX1L%2FbtrMNigeeRC%2FAAAAAAAAAAAAAAAAAAAAAJTK9Vk7vqveIQnT3aQucYHHRYL6TyKBDNWFPOs8AtfV%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DJcqCsdhN8x4uoiOno0lg%252BEceTY8%253D)