[컴퓨터비전#5/09-21] 그레디언트(엣지방향,강도), 소벨마스크 엣지검출, 엣지 잡음과 DOG & LOG 마스
[컴퓨터비전#4/09-19] 엣지 검출, 엣지 검출을 위한 미분 활용, 이미지에서의 미분 개념 [컴퓨터비전#3/09-16] 필터링( 메디안, 평균, 가우시안), 동차좌표와 동차행렬 [컴퓨터비전#2/09-14] 히스토그램,
devforyou.tistory.com
본 포스팅은 2022-09-26(월), 국민대학교 김장호교수님의 컴퓨터 비전 수업을 통해 배운내용을 정리하기 위해 작성하는 게시글입니다.
# 기계학습
컴퓨터비전에는 기계학습(머신러닝)과 같은 지식이 필요하기때문에, 다음 단원을 시작하기전에 크게크게 개념을 잡아주시기 위해서 이번 수업을 진행하셨다. 기계학습방법을 크게 4가지로 나누어 볼 수 있다.
- Supervised learning - 교사학습, training data와 desired ouputs(label)이 주어짐
- Unsupervised learning - 비교사 학습 - training data만 존재함
- Semi-supervised learning - 준교사학습 - training data와 적은양의 desired ouputs(label)이 존재
- Reinforcement learning - 강화학습 - 바둑과 같은 개념으로 단계를 넘어설때마다 새로운 길을 찾아야함.
# Supervised Learning - Regression 회귀
회귀의 방법으로 사용된 교사학습의 예를 살펴보자. 회귀는 쉽게 말해 다음 데이터의 위치를 예측하는 것이다.

시간에 따른 빙하의 면적에 관한 데이터이다. 입력값 x는 현재 하나이다. 어느정도 빨간색의 회귀선을 그려 예측이 가능하다.
# Supervised Learning - Classification
앞선 회귀의 예에서는 데이터가 딱딱 떨어지는 것이 아닌 연속된 데이터의 값이었다면 회귀의 문제에서는 데이터들이 딱딱 맞아 떨어지는 값이 나온다. 예를들어서, 데이터를 개 OR 고양이로 판별하는 것 처럼 말이다.

종양의 크기를 토대로 양성/음성 여부를 예측(분류) 할 수 있을 것이다.

그러나 이러한 1차원적인 데이터로는 오차가 발생하기 때문에, 입력값을 mulit-dimensional하게 즉 여러개(여러차원)으로 확장 시킬 수 있다. 종양의 크기와 Age(나이)의 데이터가 있다면 더욱 쉽게 분류 할 수 있을 것이다.

딥러닝의 중요한 개념 중 하나는, 이러한 feature들을 사람에 의해서 찾을 필요가 없다는 것이다. 딥러닝을 통해 모델을 만들면 여러 데이터를 통해서 분류가 되는 모델이 만들어 질 것이다. 대신 어떤 feature를 활용해서 만들어졌는지는 알 수 없게 된다.
# Unsupervised Learning - 비교사 학습
클러스터링(군집화)를 하는 것이다. 여러 개체들이 주어졌을때, 개체들을 몇개의 부분그룹(클러스터)로 나누는 과정을 뜻 한다.

비교사 학습 방버이기 때문에 데이터에 대한 라벨값은 존재하지 않는다.
이렇게 학습시킨 모델은 일반화 능력(generalization)을 가져야 한다. 즉 테스트 집합에서만 성능을 발휘하는 것이 아니라, 실제 처음 보는 데이터에 대해서도 좋은 성능을 유지시켜야 한다. 과적합(overfitting) 상황이 오면 안되는 것이다.
# Linear Functions
모델은 함수에서 최적의 파라메터를 찾아내는 행위이다. 그러기 위해서는 함수의 표현방법을 먼저 살펴보자.
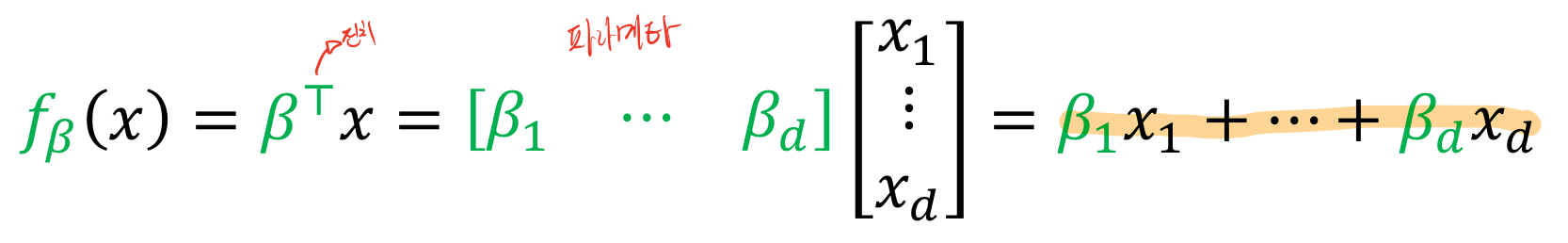
파라메타(베타)를 전치시키고 곱해주면 함수의 꼴로 표현 할 수 있다. 이러한 파라메타를 찾는 것이 목표이다. 파라메타를 표현하는 베타는 사람마다 다르게 표현 할 수 있기 때문에 베타라고 한정되어 암기하고 있지 말고 유동적이게 읽을 수 있는 능력이 필요하다 했다.

입력값 x는 한개만 존재하는 것이 아닌 R^d 즉 d는 차원으로써 3차원 4차원 등등 여러개의 값을 가질 수 있다. 이를 벡터로 표현할 수 있다.
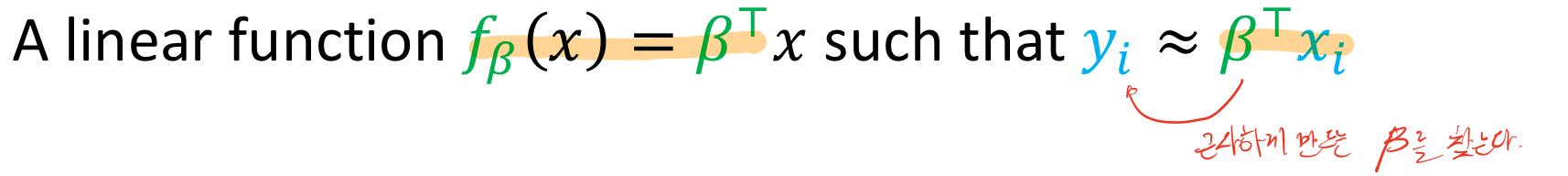
즉 가장 찾아야하는 원본 y와 비슷한 함수를 찾는 것이 목표이다. 이를 위해서는 파라메타(베타)를 가장 최적에 가깝도록 만들어야 한다.
# 손실 함수(Loss-Function or Cost-Function)
대표적인 손실함수중 하나인 MSE(Mean squared error)를 살펴보자.

오차의 제곱값을 평균을 만든다. 이를 통해서 모델이 얼마나 잘 들어맞는지를 평가할 수 있다.
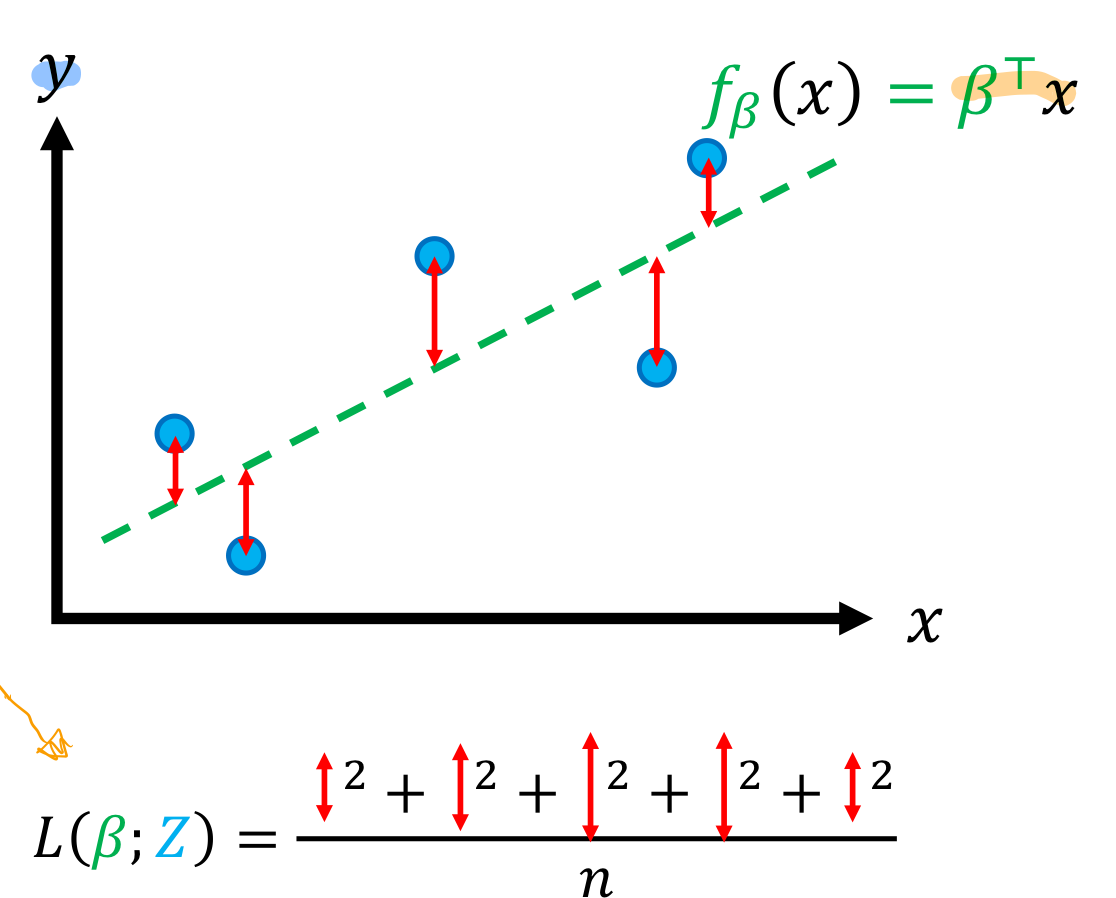
즉 이 손실함수를 가장 작게 만드는 파라메타를 찾는 수식을 풀어보면 아래와 같다.

# 파라메타와 손실함수의 관계 예제
파라메타에 따른 손실함수가 어떻게 그려지는지에 대한 예를 살펴보자.
가장 먼저 파라메타가 가장 최적인 상태를 손실함수로 표현해보자.

y = 1x, 즉 베타가 1일때 왼쪽의 그래프와 같이 그려질 것이며, 손실함수를 좌표에 표시하면 오른쪽과 같다. 손실함수가 0이라는 뜻은 딱 들어 맞는 완벽한 것이라는 뜻일 것이다.
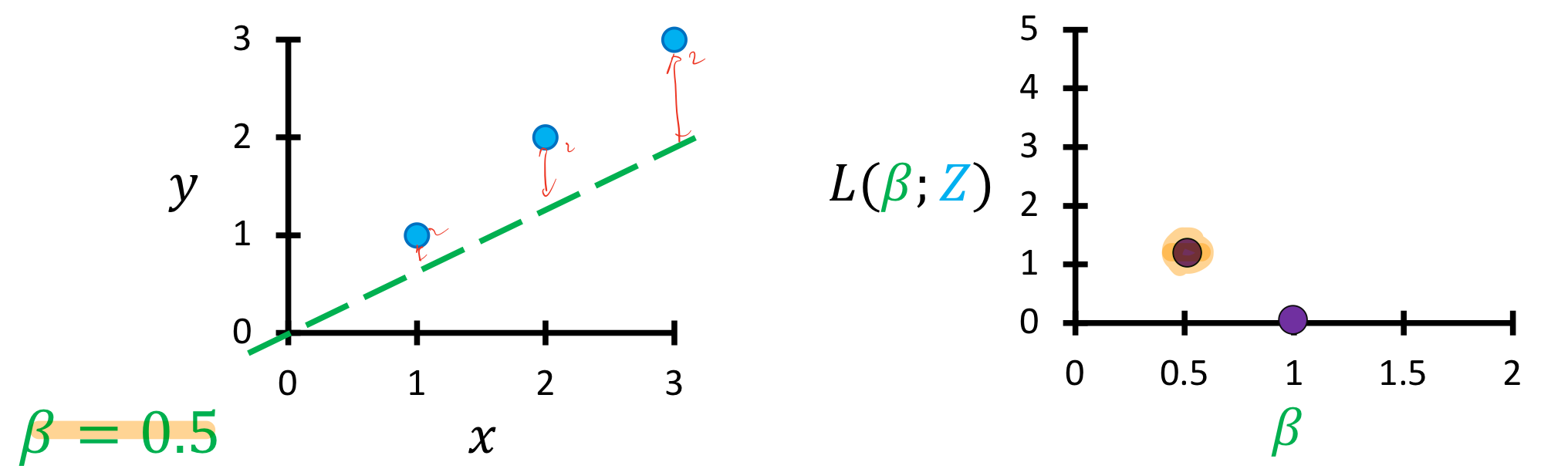
베타가 0.5, 즉 f= 0.5x의 꼴의 모델이라면, 손실함수를 계산해보면 오른쪽의 그래프처럼 표기 될 것이다.
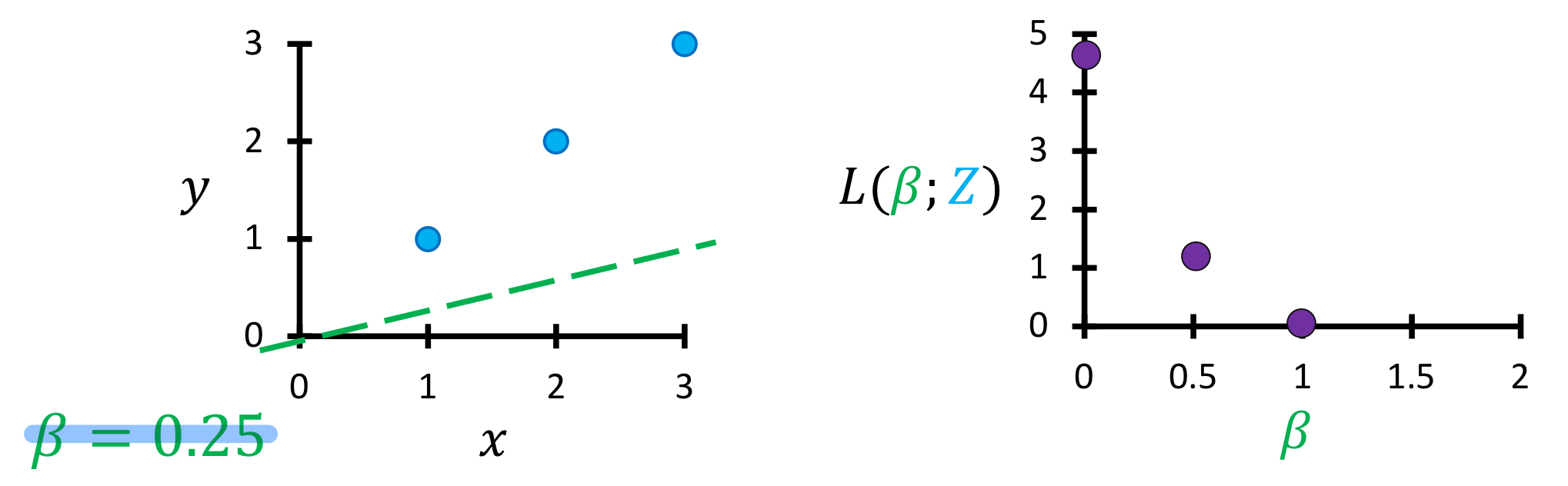
0.25의 꼴도 마찬가지이며, 이를 몇번 더 반복해보면 아래와 같은 손실함수의 그래프를 볼 수 있을 것이다.

손실함수는 오른쪽과 같은 2차원의 아래로 볼록한 형태를 가질 것이다. 이를 생각해보면 당연한게, 왼쪽 실제 모델이 1차원이고, 손실함수가 0인지점 즉 파라메타가 1일때를 기준으로 위로 올라가거나 아래로 내려가는 함수가 나온다면 똑같은 손실함수의 값이 나올 것이기 때문이다.
이를 통해 알 수 있는 점은, 손실함수를 미분하여 극소값의 지점을 찾으면 된다는 사실을 알 수 있다. 그러나 현실에서의 데이터는 이렇게 깔끔하지 않고, 모든 loss를 계산한다는 점은 비효율적이라 했다.
MSE를 통해 손실함수를 알아 봤고, 손실함수에는 이밖에도 다른 종류들이 있다.

# 마치며
머신러닝 수업에서 배웠던 내용과 유사하여 조금 수월하게 이해할 수 있었다.
'•Compter Science > Computer Vision' 카테고리의 다른 글
| [컴퓨터비전#8/10-03] 경사하강법(Gradient Descent)과 Learning Late, Stochastic Gradient Descent (3) | 2022.10.04 |
|---|---|
| [컴퓨터비전#7/09-28] Linear Regression, 벡터화, feature map (0) | 2022.09.29 |
| [컴퓨터비전#5/09-21] 그레디언트(엣지방향,강도), 소벨마스크 엣지검출, 엣지 잡음과 DOG & LOG 마스크 (1) | 2022.09.22 |
| [컴퓨터비전#4/09-19] 엣지 검출, 엣지 검출을 위한 미분 활용, 이미지에서의 미분 개념 (1) | 2022.09.20 |
| [컴퓨터비전#3/09-16] 필터링( 메디안, 평균, 가우시안), 동차좌표와 동차행렬 (1) | 2022.09.19 |
![[컴퓨터비전#6/09-26] 기계학습의 종류와 개념, 손실함수, 손실함수와 파라메타](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FoZILw%2FbtrNeJbNvZs%2FAAAAAAAAAAAAAAAAAAAAALE8akn4-4e1f6c7R9i1Oinap129LPv6D4f7d0qqBpOM%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DQnfru3sje9XcYOFmuLmTn1ed%252Fio%253D)