[컴퓨터비전#2/09-14] 히스토그램, 히스토그램 평활화, 점연산(선형,비선형,디졸브),영역연산(상관,
본 포스팅은 2022-09-14(수), 국민대학교 김장호교수님의 컴퓨터 비전 수업을 통해 배운내용을 정리하기 위해 작성하는 게시글입니다. [컴퓨터비전#1/09-07] 샘플링과 양자학, PTE, 정밀도(Precision), 재
devforyou.tistory.com
본 포스팅은 2022-09-16(금), 국민대학교 김장호교수님의 컴퓨터 비전 수업을 통해 배운내용을 정리하기 위해 작성하는 게시글입니다.
# 선형과 비선형

본 수업에서 선형이 매우 중요한 개념임을 알 수 있다. 말그대로 선형함수는 직선으로 그려지고, 비선형은 직선이 아닌 형태로 그려진다.
# 메디안 필터
솔트페퍼 잡음을 제거하는데 효과적인 메디안 필터는 영역 연산 중 비선형 연산이다. 선형, 비선형의 의미를 두기보단 이번단원에서 알아보는 필터(Filters)의 개념을 이해하기 위한 간단한 예제를 살펴보자.

(b)솔트페퍼 잡음이 존재하는 이미지에 메디안 필터가 적용되면 잡음이 사라지는 것을 알 수 있다. 어떻게 가능한걸까?
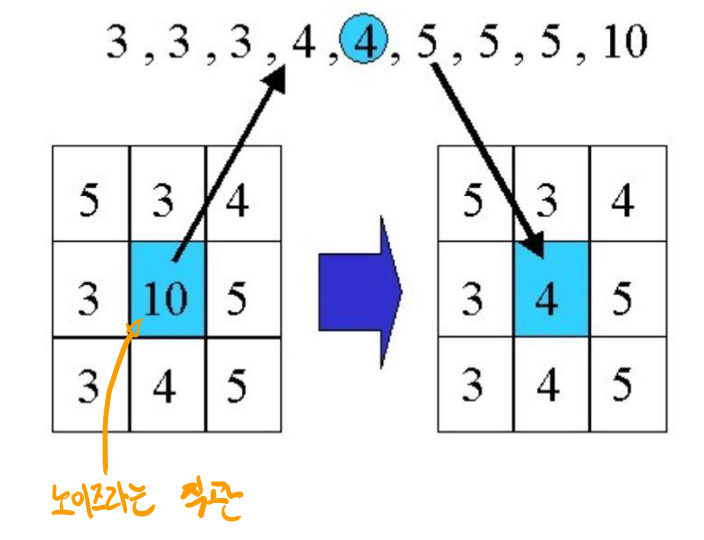
명도는 낮을수록 어둡고, 높을수록 밝다. 아마 "10"이라는 것은 직관적으로 노이즈가 존재하는 곳이라고 알 수 있을 것이다. 그럼 그 주변의 5,3,4,3,10,5,3,4,5를 순서대로 나열하고 중간값으로 해당 노이즈부분을 대체한다. 이것을 통해 이미지가 필터링 되어 잡음이 사라지는 것이다.
# 동차 좌표(Homogeneous coordinate) 와 동차 행렬
비선형을 선형을 통한 연산을 하기 위해서 동차 좌표와 동차행렬을 사용한다.
## 동차 좌표

(3,5)에서 1을 추가하여 동차 좌표를 만든다. (3,5,1)을 통해 차원을 확장 시킨다.
## 동차 행렬
이렇게 만들어진 동차 좌표를 동차행렬연산을 통해 손쉽게 이동, 회전, 크기, 기울임과 같은 연산을 할 수 있다.

간단히, 이동의 예를 보면 아래와 같이 손쉽게 이동된 것을 알 수 있다.

# 동차행렬을 사용하는 이유
먼저 기하 연산은 비선형 연산이다. 그러나 동차좌표를사용하면 이를 선형연산으로 바꿀 수 있게되고 수학의 수식(선형대수...)들을 이용해서 손쉽게 변환이 가능하기 때문에 동차행렬을 사용한다.
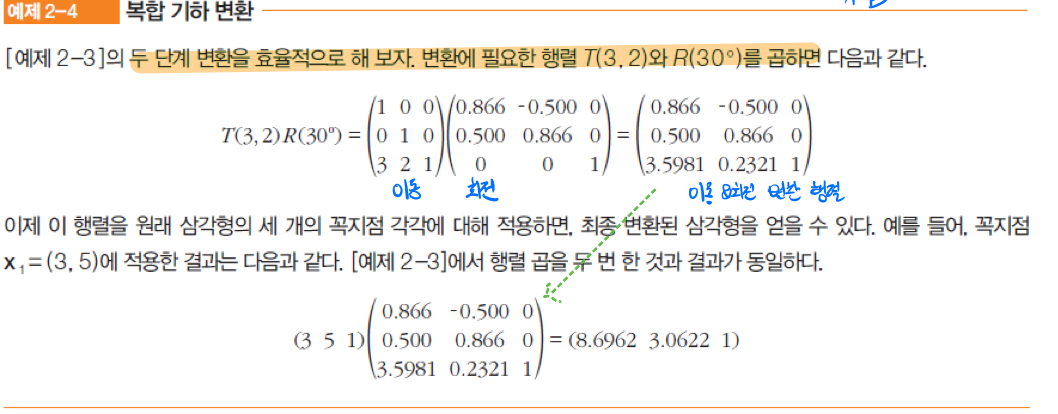
아래는 이동후 회전시키는 예제이다.

(3,2)를 (6,7)로 이동시키고 이를 회전시킬 수 있는 것을 볼 수 있다.
여기서 중요한 사실은 행렬곱셈은 결합법칙이 적용된다는 것이다. A*B*C = A*(B*C)
그렇기 때문에 위 2-3의 예제를 조금더 쉽게 할 수 있다. 이동과 회전시키는 행렬을 미리 계산한 후, 그 행렬을 각 꼭지점에 곱해주면 된다.
만일 구해야하는 꼭지점이 무수히 많다면 연산이 줄어들게 되기 때문에 매우 효율적일 것이다.
# 이미지는 함수이다
사고를 확장시켜 이미지는 함수라고 생각해 볼 수 있다. R,G,B의 좌표값의 경우 아래와 같이 표현 할 수 있을 것이다. 이렇게 수학적으로 생각해야지 수학을 도구로 하여 사용 할 수 있기 때문이다.

터미네이터 이미지를 좌표계의 표현된 데이터들로 봐보면, 아무 의미 없는 것이 아닌, 터미네이터 얼굴이 보이는 것을 볼 수 있다.

f(x,y)에 좌표값을 넣으면 나오는 명도값이 z축으로 표기 될 것이고 터미네이터의 얼굴이 보인다!
샘플링과 양자화를 통해서 아날로그의 이미지(?)를 디지털로 전환시킨다. 고화질의 사질을 얻기위해서는 높은 픽셀로 샘플링을 하면 더 선명한 사진이 나오겠지만, 이는 연산해야하는 양이 기하급수적으로 증가한다.
# 필터링

## Mean Filtering
Mean(평균) Filtering을 이용해서 노이즈를 어떻게 제거하는지 봐보자.
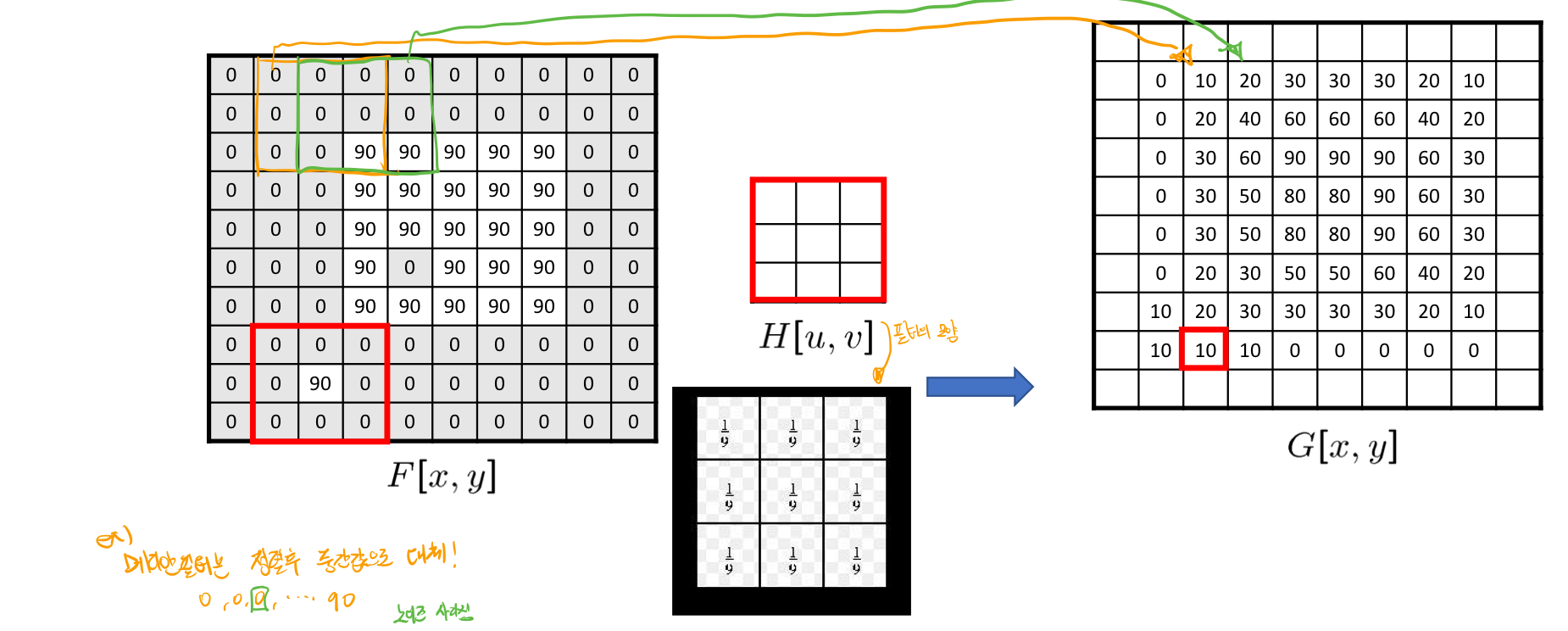
윈도의 내에서 평균낸 값을 더해줘서 변환시킨다. 즉 해당 값은 주변과 비슷해지게 된다.
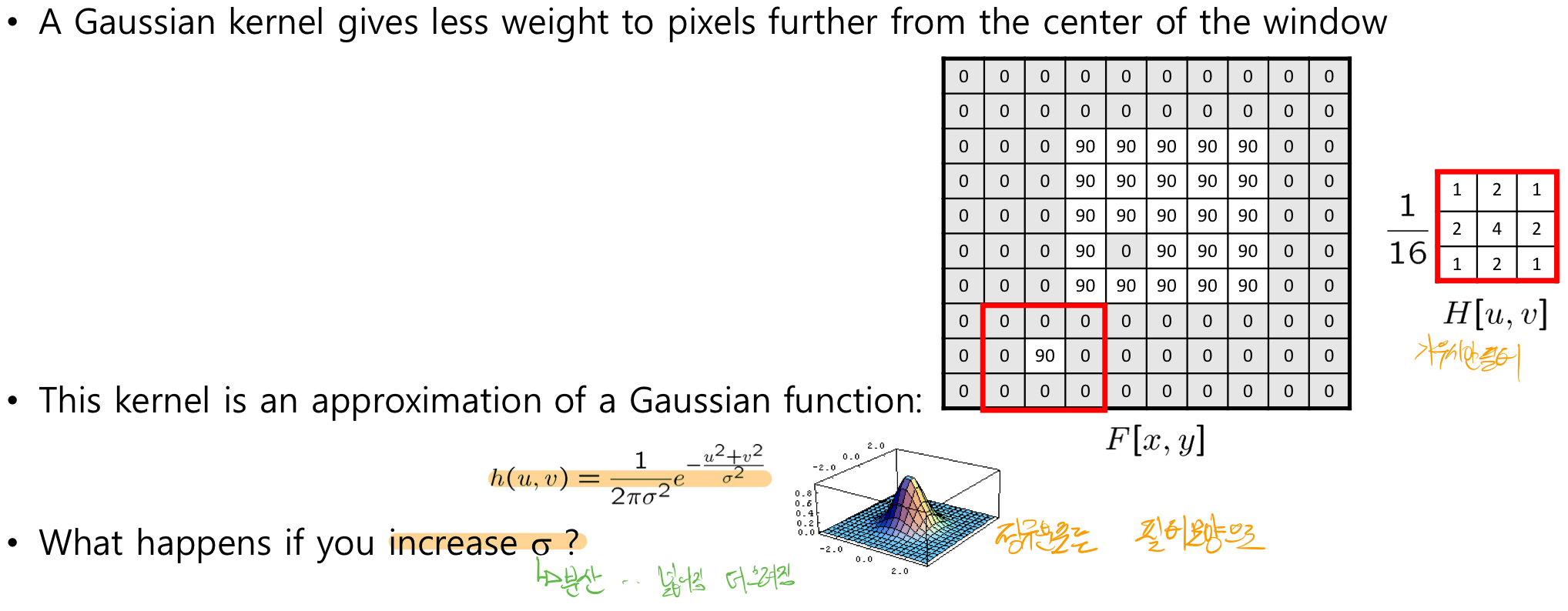
## Gaussian filtering (가우시안)
가우시안 필터를 사용하면 블러효과를 낼 수 있다. 정규분포에서의 분산의 값을 이용해 변형한다. 분산의 값이 클 수록 범위가 넓어지기 때문에 더 흐려진다.
'•Compter Science > Computer Vision' 카테고리의 다른 글
| [컴퓨터비전#6/09-26] 기계학습의 종류와 개념, 손실함수, 손실함수와 파라메타 (2) | 2022.09.28 |
|---|---|
| [컴퓨터비전#5/09-21] 그레디언트(엣지방향,강도), 소벨마스크 엣지검출, 엣지 잡음과 DOG & LOG 마스크 (1) | 2022.09.22 |
| [컴퓨터비전#4/09-19] 엣지 검출, 엣지 검출을 위한 미분 활용, 이미지에서의 미분 개념 (1) | 2022.09.20 |
| [컴퓨터비전#2/09-14] 히스토그램, 히스토그램 평활화, 점연산(선형,비선형,디졸브),영역연산(상관,컨볼루션) (0) | 2022.09.15 |
| [컴퓨터비전#1/09-07] 샘플링과 양자학, PTE, 정밀도(Precision), 재현율(Recall), 정확도(Accuracy) (0) | 2022.09.08 |
![[컴퓨터비전#3/09-16] 필터링( 메디안, 평균, 가우시안), 동차좌표와 동차행렬](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fb7HxAj%2FbtrMrw5NrvB%2FAAAAAAAAAAAAAAAAAAAAAMBFCAk--PWGUhXPYgqzR8rkLtKC7dUtKZ5AdE8d_trt%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3DJPgXafYVgQ2X8Oc80O%252FtnOIQi9k%253D)