[인공지능#6/10-03]
devforyou.tistory.com
본 포스팅은 2022-10-05(수), 국민대학교 이재구 교수님의 인공지능 수업을 통해 배운내용을 정리하기 위해 작성하는 게시글입니다.
# 시작하기 전
해당일(10-05)에 예비군이 있어서 수업을 듣지 못했다. 교수님께서 작년 녹화강의를 올려주셨다. 또 10-03에 했던 확률관련 수업은 다시 한번 공부한다음에 포스팅해야할거 같아서 먼저 포스팅한다.
# 정보이론
어떠한 정보를 신호로 처리해서 보낼때 그 최적의 코드를 디자인하고, 기대길이를 계산하기 위해 등장한 개념이다. 사건(event)이 지닌 정보(불확실성)을 정량화 할 수 있을까? 정보이론의 기본 원리는 확률이 작을수록 많은 정보를 내포하고 있다는 것이다. "아침에 해가 뜬다"와 "오늘 아침에 일식이 있었다"라는 두 사건 중 "오늘 아침에 일식이 있었다"라는 사건이 더 많은 정보를 가지고 있을 것이다. 아침에 해는 항상 뜨기 때문이다. 이 이야기가 와 닿지 않을 수 있다. 대화 예제를 통해 잘 일어나지 않은 사건이 왜 더 많은 정보를 가지고 있는지에 대해서 살펴보자.
## 대화 예제

길동이와 쇠똥이의 대화를 살펴보자. 이 대화에서 "뭐함?"이라는 말이 가장 많이 쓰인다. 길동이는 쇠똥이와의 대화가 신물이 났는지 마지막에 회심의 "ㅗ"을 날리고 대화를 종료 했다. 우린 111 또는 0으로 이 대화를 표현해야한다고 치자.
- "뭐함"을 111로 "ㅗ"을 0으로 하면 이대화는 어떻게 표현 될까? 111 111 111 111 111 111 111 111 0으로 표현될 것이다.
- "뭐함"을 0으로 "ㅗ"을 111로 하면 이 대화는 어떻게 표현 될까? 0 0 0 0 0 0 0 0 111으로 표현 될 것이다.
즉, 잘 일어나지 않는 사건(unlikely event)에 111이라는 더 많은 정보를 표현 함으로써 정보의 길이를 짧게 할 수 있었다. 이를 정보이론에 설명에 빗대어 보면, 확률이 작을수록 많은 정보를 가진다. 자주 발생하는 사건보다 잘 일어나지 않는사건의 정보량이 많다.라고 해석 할 수 있을 것 이다.
## 자기 정보(self information)

그렇다면 정보량은 위와 같은 수식에 의해서 표현 될 수 있다.

다시 말해 어떠한 한 사건에 대해서 표현하면 위와 같다. 로그의 밑이 2인 경우는 bit를 자연 상수인 경우는 나츠(nat)를 표현한다고 한다.
아래 예제를 살펴보자. 두 사건이 있을때 어떠한 사건의 정보량이 더 클까? 위에서 배웠던 것을 되새기면, 확률이 작을수록 많은 정보량을 가져야 할 것이다.

동전의 1/2사건과 주사위의 1/6사건 중 주사위의 사건이 더 확률이 작기 때문에 높은 정보량을 가진다.
아래 이미지를 보면 발생확률에 따라서 정보비트가 커짐을 알 수 있다.
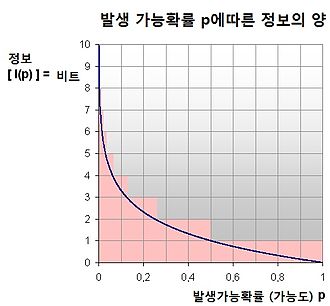
## 엔트로피
엔트로피는 간단히 말해 정보를 표현하는데 필요한 최소 평균 자원량을 뜻한다. 즉, low boundary를 잡아주는 것이 된다.
엔트로피는 전체 사건 정보량의 기대값이다. 우리는 확률변수의 기대값(평균)을 도수*확률의 합을 통해서 구했다. 이와 같이, H(x) 또한 비슷한 방법으로 구할 수 있다.

이산 확률분포와 연속확률분포에 대해서 정리하면 아래와 같다.

## 엔트로피가 최대일때
그렇다면 엔트로피가 최대일때는 어떻게 될까? 즉 사건의 분포가 결정적이라면 해당 확률분포의 불확실성 정도를 나타내는 엔트로피는 낮아진다. 그러나 분포(확률)이 균등하다면 엔트로피가 가장 높아질 것이다. 어느 사건이 나올지 모르기 때문이다. 아까본 ##대화 예제 를 생각해보자 대화가 "뭐함?" "ㅗ"이 계속해서 반복된다면 111과 0을 어디에 주던 가장 긴 경우가 될 것이다.
동전 앞뒤 발생 확률(1/2)일 경우의 엔트로피를 봐보자.

## 교차 엔트로피(Cross-Entropy)와 KL-Divergence(발산)
두 확률 분포 P와 Q 사이의 엔트로피를 나타낸다. 여기서 Q에 우리가 생각한 정보량을 넣어본다고 생각하면 된다.

그렇다면 우리가 생각한 값과 원래 최소값(엔트로피)의 어떠한 관계를 이용한다면 우리가 생각해낸 Q가 좋은 값인지를 알 수 있을 것이다. 엔트로피와 크로스엔트로피를 한번더 생각해보자. 크로스엔트로피의 값이 엔트로피의 값보다 최적일때는 같을 것이며 대부분의 경우는 클 것이다. 그렇기 때문에 크로스엔트로피에서 엔트로피의 값을 빼준다. 그러면 KL-Divergence을 구할 수 있다.

그러면 우리는 로그의 차 계산식에 의해서 아래와 같은 KL-Divergence의 식을 구할 수 있다.

다시 크로스 엔트로피로 돌아와 식을 전개해보자 그러면 KL-Divergence와 크로스 엔트로피사이에는 깊은 관련이 있음을 알 수 있다.

즉 크로스 엔트로피를 손실함수로 사용하는 경우에는 원래 데이터 분포 P(x)와 우리가 추정한 데이터 분포 Q(x)간의 차이를 최소하하는 다시 말해 KL-Divergence를 최소화함과 동일하다는 결론에 달할 수 있다.
### 크로스 엔트로피와 KL발산을 이용한 예제

최적화 단원에서는 경사하강법을 배웠는데 지난 컴퓨터 비전시간에 배운 경사하강법과 거의 똑같은 것을 공부했다. 참고하자!
[컴퓨터비전#8/10-03] 경사하강법(Gradient Descent)과 Learning Late, Stochastic Gradient Descent
[컴퓨터비전#7/09-28] Linear Regression, 벡터화, feature map [컴퓨터비전#6/09-26] 기계학습의 종류와 개념, 손실함수, 손실함수와 파라메타 [컴퓨터비전#5/09-21] 그레디언트(엣지방향,강도), 소벨마스크 엣
devforyou.tistory.com
# 최적화
## 경사하강법
수학의 최적화 : 어떤 상황에서 함수의 최대치 혹은 최소치를 찾는 것
기계학습에서 최적화 : 학습 모델의 매개변수 공간을 탐색하여 목점함수가 최저가 되는 최적점을 찾음.

이계도함수가 0인지점을 찾아 도함수의 최저점을 찾을 수 있었다. 그러나 찾아야하는 매개변수가 많아질수록 이러한 지점을 찾는 것이 어려워지고 경사하강법을 사용하여 찾을 수 있게 됐다. 특히 경사하강법은 미분을 이용하여 갱신의 갱신을 반복하여 찾아가는 과정이다.
경사하강법에 대한 개념은 컴퓨터 비전게시글을 참고하고 여기선 다루지 않도록 하겠다!
# 야코비언 행렬과 헤세 행렬

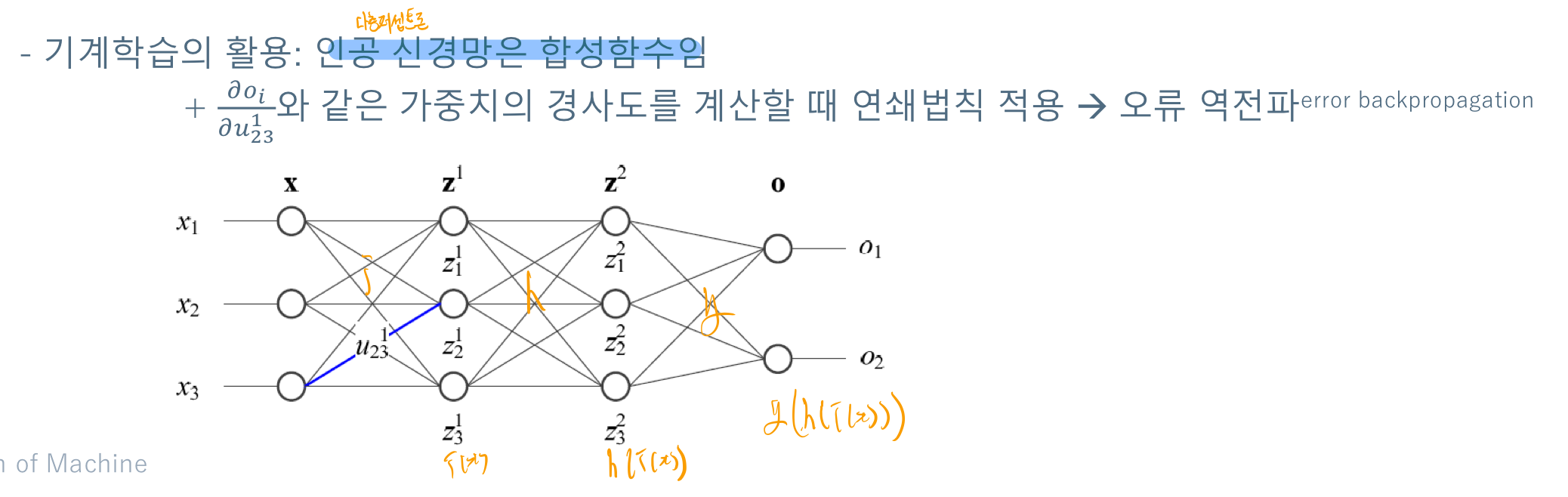
# 기계학습의 활용과 미분의 연쇄법칙

인공 신경망은 결국 합성함수이다. 이번강의에서는 이러한게 있다는 정도만 알려주셨다. 이러한 합성함수의 미분과정을 통해서 무엇인가를 찾게 되는데, 합성함수의 미분이 사용된다고 한다.
# 참고
정보이론 기초 · ratsgo's blog
이번 글에서는 정보이론(Information Theory)의 기본 개념들을 살펴보도록 하겠습니다. 이 글은 Ian Goodfellow 등이 집필한 Deep Learning Book과 위키피디아를 정리했음을 먼저 밝힙니다. 그럼 시작하겠습니
ratsgo.github.io
'•Compter Science > Artificial Intelligence' 카테고리의 다른 글
| [인공지능#9/10-31] 깊은 신경망(DNN)과 CNN 맛보기 (0) | 2022.10.31 |
|---|---|
| [인공지능#8/10-12] 인공신경망, 퍼셉트론 개념 (0) | 2022.10.13 |
| [인공지능#6/10-03] 확률과 조건부 확률, 베이지 정리를 이용한 IRIS 추정 (0) | 2022.10.08 |
| [인공지능#5/09-28] 선형대수(벡터,행렬,분해,놈,선형결합..) (0) | 2022.10.01 |
| [인공지능#4/09-21] 학습모델(검증, k-교차검증)선택, 규제(데이터 증대, 가중치 패널티), 인공지능 기본수학 (1) | 2022.09.25 |
![[인공지능#7/10-05] 정보이론과 엔트로피, 크로스엔트로피, KL-Divergence, 경사하강법](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FdwnbT9%2FbtrN6mmqSjF%2FAAAAAAAAAAAAAAAAAAAAAA09Ebw4u1KhY5n4aZCPKeWnh77QTObKlHy6GP6Wb8mK%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DMK%252FOZdBDW%252Fp%252BYScFFzwT7lpXABg%253D)