[인공지능#1/09-07] 인공지능의 정의, 교사학습, 비교사학습, 강화학습, 준교사학습, 모델의 유형
본 포스팅은 2022-09-07(수), 국민대학교 이재구 교수님의 인공지능 수업을 통해 배운내용을 정리하기 위해 작성하는 게시글입니다. # 인공지능(Artificial Intelligence) 정의 인간의 학습, 추론, 지각, 자
devforyou.tistory.com
본 포스팅은 2022-09-14(수), 국민대학교 이재구 교수님의 인공지능 수업을 통해 배운내용을 정리하기 위해 작성하는 게시글입니다.
# 특징 공간
특징공간은 관측값들이 있는 공간을 뜻한다. 특징공간은 특징변수에 의해서 결정된다. 예를들어 특징 변수가 두개이면 2차원의 공간, 세개이면 3차원의 공간 N개이면 N차원의 공간이 형성된다. 이러한 공간을 나타낼때, 목표값을 하나의 축으로 더해서 표현 할 수도 있다.
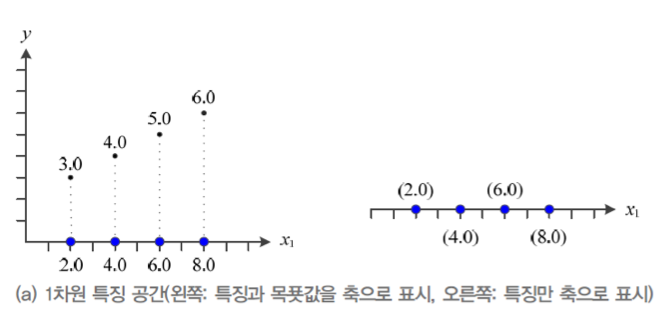
예를들어, 다음과 같이 x1,x2의 특징벡터를 가지는 데이터를 특징 공간에 표현하면 아래와 같다.

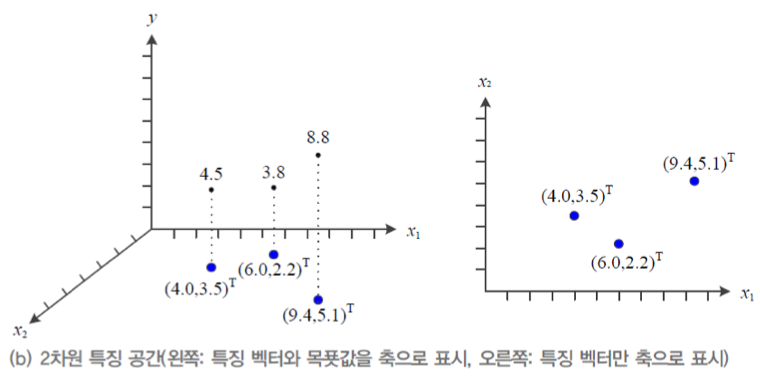
목표값을 표현하지 않으면 두번째 그래프처럼 2차원 공간이 나오고, 목표값을 표현하면 3차원의 공간으로 표현 할 수 있다.
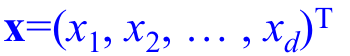
이런 d-차원 데이터의 특징 벡터는 위와 같이 표시 한다.
## 데이터와 차원공간

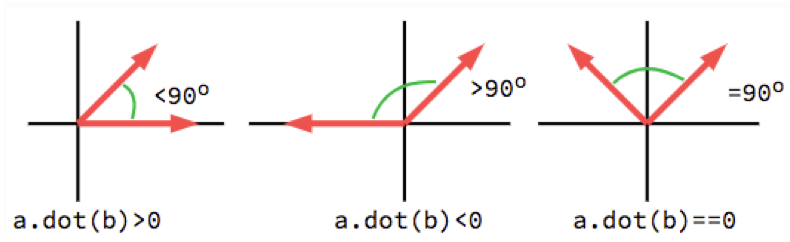
필기 숫자 집합에서의 데이터들을 특징공간으로 옮겼다고 가정해보자. "1"과 "2"는 우리가 한눈에 보기에도 뭔가 비슷하다는 생각이 들지 않지만, "2"와 "3"을 비교해보면 2에서 한획만 긋는다면 3이 될것 같다는 생각을 해 볼 수 있다. d-차원의 특징공간에서의 이러한 생각은 거리와 유사도로 표현 될 수 있다. 벡터값에는 크기와 방향을 지니고 있다는 사실을 상기하자.
비슷하면 비교적 가까운 거리를 가질 것이며 이것은 벡터에서 크기 성분을 표현한다.

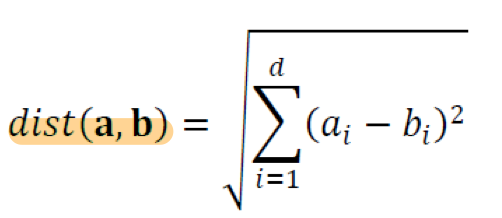
비슷하면 비교적 비슷한 방향을 가질 것이며 이를 유사도, 내적을 통해 표현한다. 벡터에서 방향 성분이다.
데이터를 선형 변환(linear transformation)을 통해서 원래 가지고 있던 특징공간에서의 데이터에서 보이지 않던 특징을 추출하기 위한 가공을 한다.
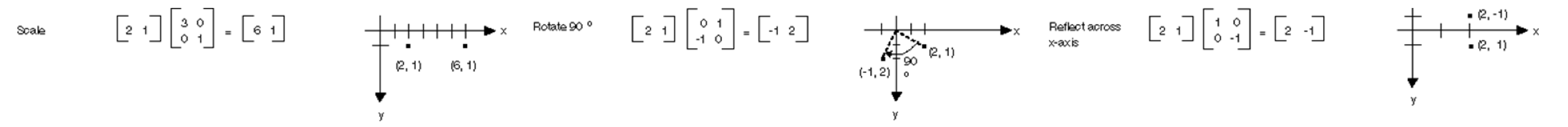
# 데이터 차원의 저주(curse of dimensionality)
데이터의 차원이 증가할수록 특징공간의 크기(부피)가 기하급수적으로 증가하게 된다. 차원이 증가하게됨에 따라 변수(특징벡터)가 늘어나게 되고, 해당 차원에서 학습해야할 데이터 수가 적어지게 되기 때문에 기계학습을 위한 데이터의 개수가 기하급수적으로 증가하게 되고 어렵게 되는 문제이다. 즉 차원이 증가할수록 빈공간이 많아진다는 것이다.
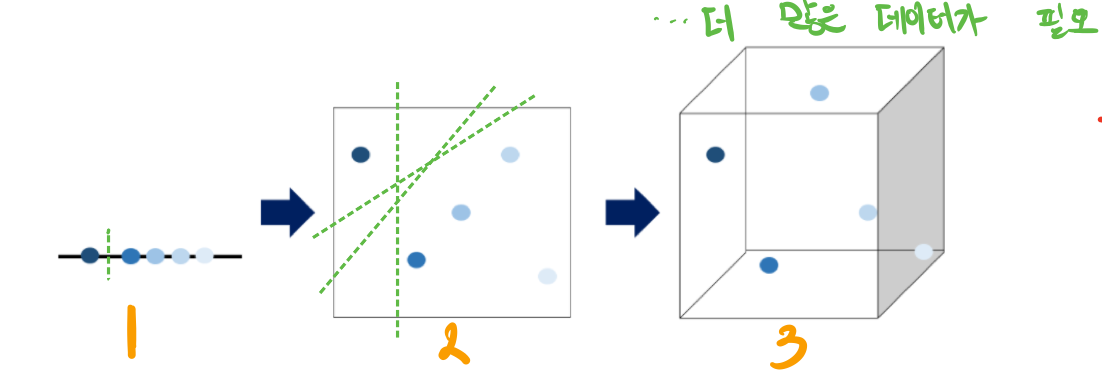
같은 데이터를 1차원, 2차원, 3차원 특징공간에 옮겨 놓은 모습이다. 초록 점선으로 표기한 것을 살펴보면, 1차원일때와 2차원일때와 3차원일때 그을 수 있는 선의 개수가 많아진다. 즉 부피가 커지고 학습해야할 곳이 더 늘어나게 된다.
그러나 차원의 저주라는 설명은 반은 맞고 반은 틀렸다고 볼 수 있다. 아래의 예제를 살펴보자.
MINIST 784차원 공간을 가진다. 그러나 훈련집합은 6만개로 차원의 비하면 매우 적은양이지만 성능을 예상할 수 있는 이유는 무엇일까?
- 고차원 특징 공간에서 실제 데이터가 발생하는 영역은 매우 희소한 공간이다. 실제 데이터는 뭔가 유의미한 데이터가 발현된다.

- 일정 규칙에 의해 차원 간의 매끄럽게 변화하는 양상을 가진다. 즉 데이터가 유사한 규칙에 의해 발생된다.

- 고차원의 데이터는 관련된 낮은 차원의 공간의 조합으로 구성된다. 매니폴드(manifold : 많이 + 접힘)
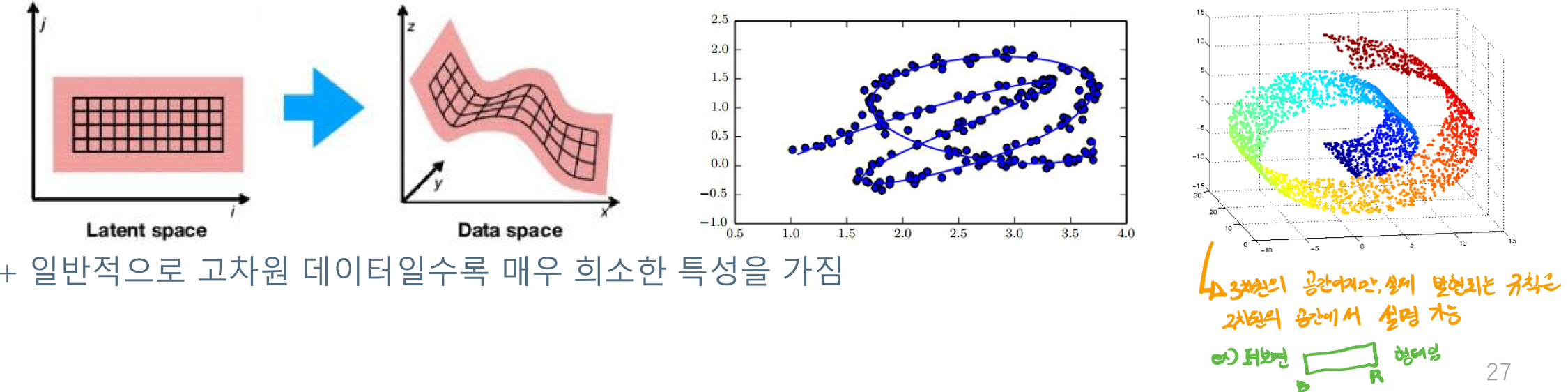
즉, 고차원에서 생성된 데이터일지라도 막상 보면 저차원에서 그 규칙을 찾을 수 있다는 것이다.
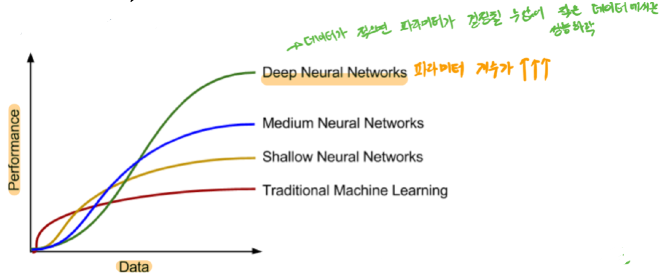
결론은 데이터의 양이 기계학습 모델에서 중요하다는 것이다. 데이터가 많아야지 파라미터를 결정 할 수 있다.
# 기계학습의 개요
## 신용승인 사례
강의에서는 신용승인 사례를 통해서 기계학습의 개요를 설명해 주셨다. 은행은 빛을 잘 갚는 사람에게 돈을 빌려주는 것이 이득이기 때문에, 지금까지 돈을 빌려주고 그 결과의 데이터들을 통해 학습을 한다. input과 output을 모두 알기 때문에 교사학습의 방법이 될 것이다.

다음과 같은 데이터 셋들과 사례여부의 결과값이 존재한다. 돈을 잘 갚을 것 같은 능력을 찾아 보자.

다음과 같이 도식화를 한다. 결국 target을 찾아내야 하는 것이다. 가설 X->Y는 처음부터 맞지는 않지만 점점 맞아 갈 것이다.
## 구체화
신용 승인 사례의 교사학습 방법을 조금 더 구체화 해보도록 하겠다.
나이(age)와 연봉(annual salary)가 신용 승인과 조금 관계가 있지 않을까에 대한 가설을 세우고 데이터로 정한다. 그리고 이 값들을 공간에 표현해 본다.
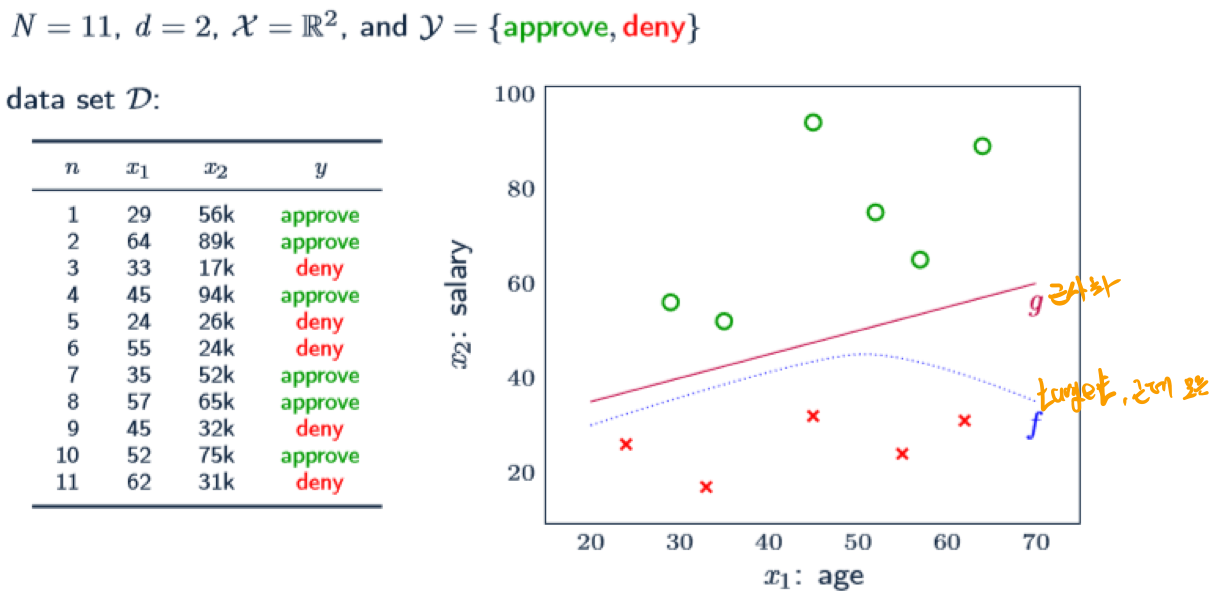
아마 정확한 target은 파란 점선(f)와 같을 것이지만 우린 정확한 값을 알아 낼 수 없다. 다만 근사화 된 g라는 값을 알아 낼 것이다.
이렇게 학습데이터로부터 target을 찾아내는 모델을 만드는 것이 기계학습의 목표이다.
## 기계학습의 개요 - 교사학습일 경우
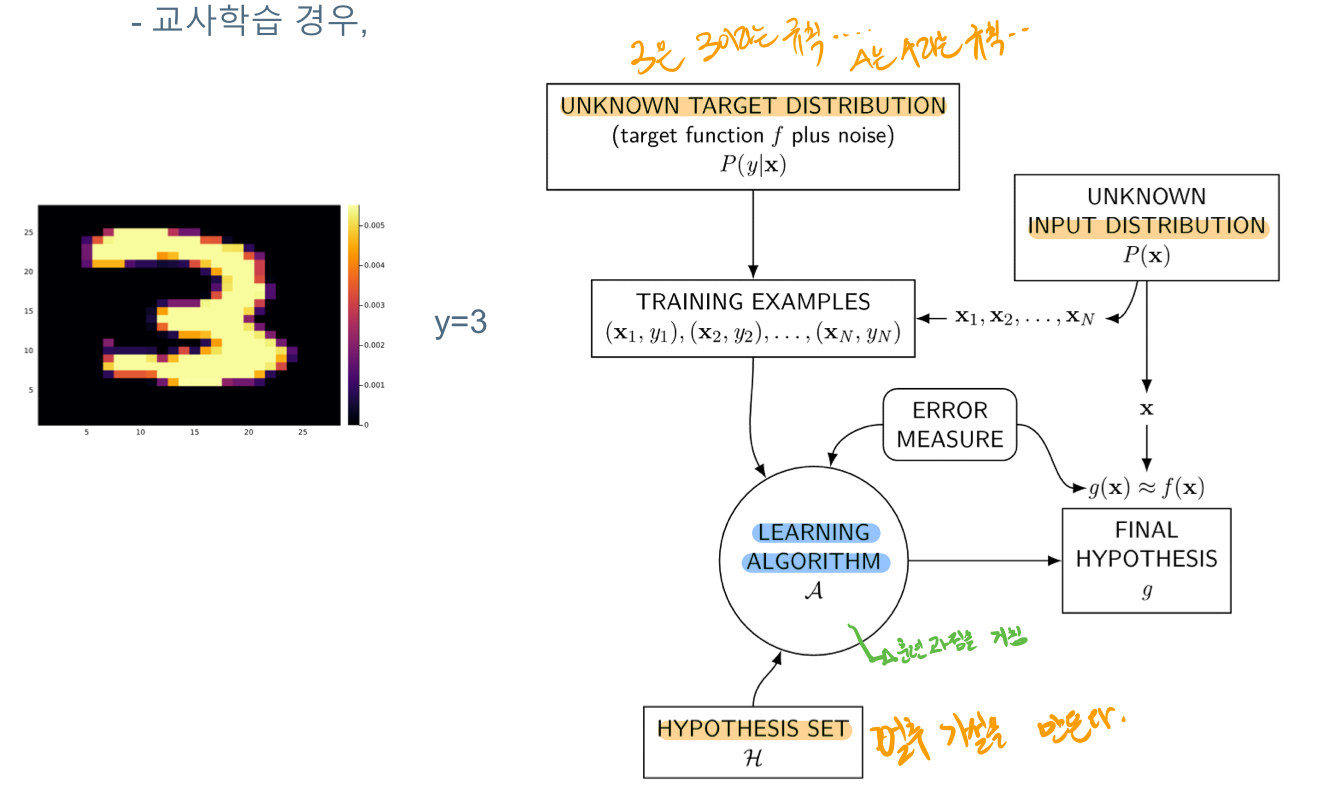
즉 근사화된 비슷한 target을 찾기 위해서, 데이터셋들과 가설 그리고 오차를 측정해가면서 모델을 만든다.
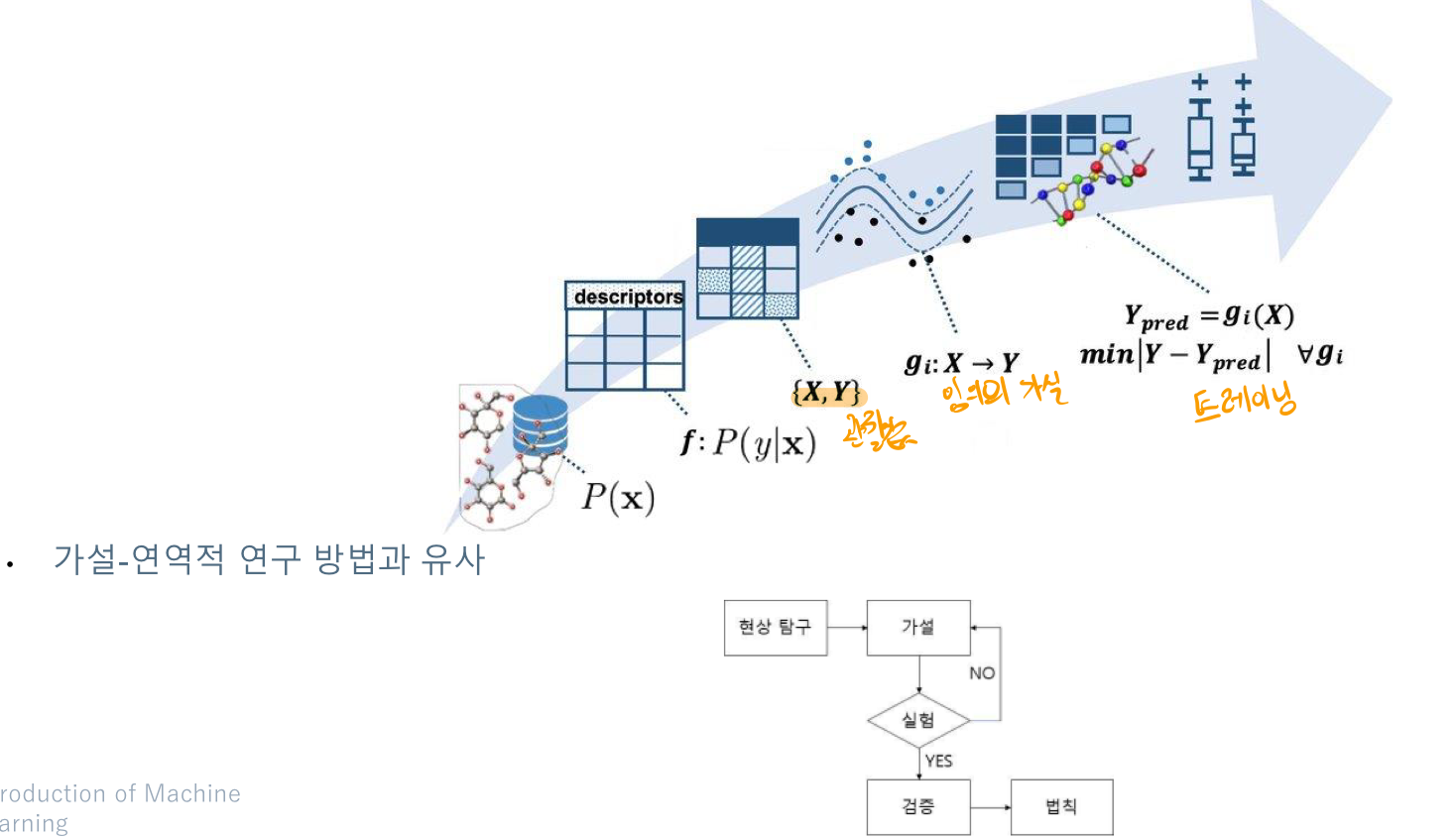
# 예측 문제
- 회귀 : 목표치가 실수 ( 연속적인 값)
- 분류 : 목표치가 부류(class) 이며 불연속적인 값
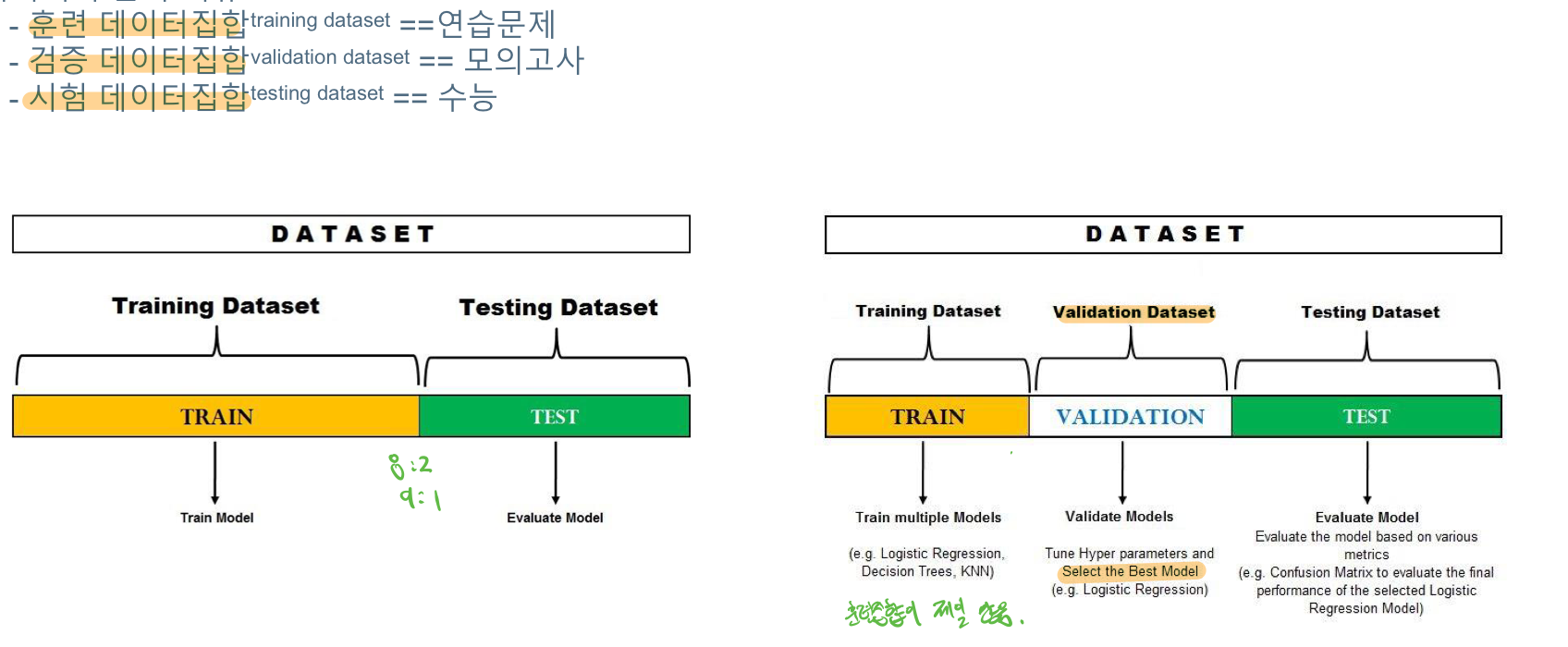
# 데이터의 구분과 비유
# 목적함수와 훈련 과정
목적함수는 정량적인 성능 판단 지표, 그 중 평균 제곱 오차(Mean Squared Error)가 존재한다.
학습 모델이 어느정도의 예측실력을 가지는지를 평가할 수 있다.
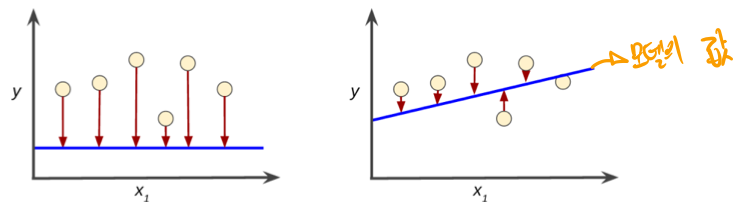
1번의 경우 모델의 값에 대한 MSE가 큰 값을 가질 것이고, 2번의 경우 상대적으로 MSE가 작은 값을 가지기 때문에 2번이 더 좋은 모델이라고 평가 할 수 있다는 것이다.
## 훈련 과정
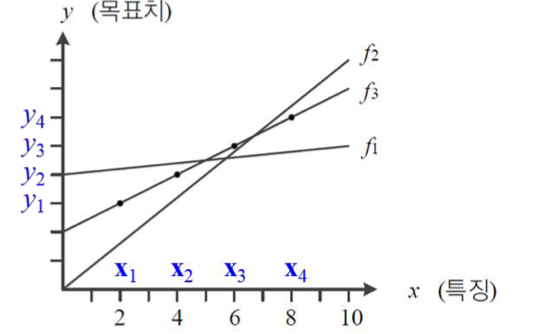
가설을 통해 직선의 모델을 채택한 경우, y = wx + b에서 2가지의 학습 매개변수 w,b를 찾아야 한다. 이 정확한 w,b를 학습을 통해 찾을 수록 좋은 모델이 될 것이다. 이것을 기계학습의 훈련 과정이다. f1 -> f2 -> f3으로 최적의 학습 모델을 찾게 된 경우이다.
# 마치며
강의시간보다 정리하는게 훨씬 오래 걸린다. 그래도 이번 수업내용을 정리하면서 모르고 헷갈렸던 것들이 대부분 해결 됐기에 뿌듯하다!
'•Compter Science > Artificial Intelligence' 카테고리의 다른 글
| [인공지능#6/10-03] 확률과 조건부 확률, 베이지 정리를 이용한 IRIS 추정 (0) | 2022.10.08 |
|---|---|
| [인공지능#5/09-28] 선형대수(벡터,행렬,분해,놈,선형결합..) (0) | 2022.10.01 |
| [인공지능#4/09-21] 학습모델(검증, k-교차검증)선택, 규제(데이터 증대, 가중치 패널티), 인공지능 기본수학 (1) | 2022.09.25 |
| [인공지능#3/09-19] 기계학습 훈련과정, 오버피팅(overfitting)과 언더피팅(underfitting), 편향(bias)과 변동(variance) (0) | 2022.09.20 |
| [인공지능#1/09-07] 인공지능의 정의, 교사학습, 비교사학습, 강화학습, 준교사학습, 모델의 유형 (0) | 2022.09.09 |
![[인공지능#2/09-14] 특징공간, 차원의 저주, 기계학습의 전반적 개요 및 목적함수의 의미와 훈련과정](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FGwQJQ%2FbtrMnJYnnjg%2FAAAAAAAAAAAAAAAAAAAAACUh4WDu2Z4EoAqDgeARGRHJqL0TIidNHG6TtybO3p20%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1767193199%26allow_ip%3D%26allow_referer%3D%26signature%3DUjsxZ3wVO%252FbucehxMk8%252B3JlWG1M%253D)